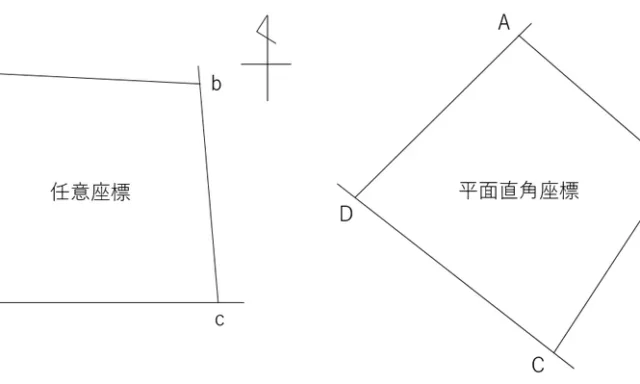
早くて正確に!複素数による測量計算ミニ講座⑥点の移動
本ページにはプロモーションが
含まれていることがあります
複素数ミニ講義の6回目です。
今回は,「点の移動」です。
どういうことかというと,『既知の点からの「方向」と「距離」が分かっている新点の座標値を求める』ってのをやります。
★★★★★★★★★★★★★★★★★★★★★
テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓
アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】
▼ サンプル講義の動画もどうぞ!
amazon kindleの電子書籍はコチラ↓
中山祐介【複素数で解く!関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い!使える! Kindle版】
★★★★★★★★★★★★★★★★★★★★★
■点の移動(基礎)
それでは,複素数モ-ドでの座標の取扱いに慣れるため,点を決まった距離と決まった方向に移動させた座標値を求めてみましょう。
T1を「x」に,T2を「y」に記憶させてあることを前提にします。
前の記事で記憶させていますが,すでにメモリが変わってしまった方は,前の記事をご参考に,T1を「x」に,T2を「y」に記憶させてください。記事を見ずに自分でやってみるのもいいでしょう!
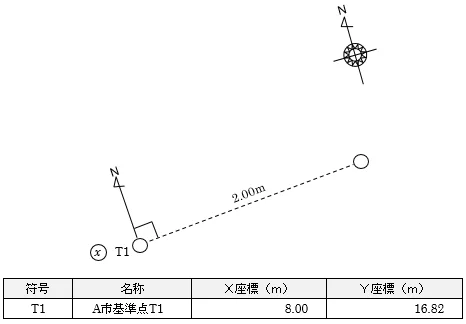
さて,まずは,T1を座標北から90度方向に2.00m移動させた点の座標値を求めます。
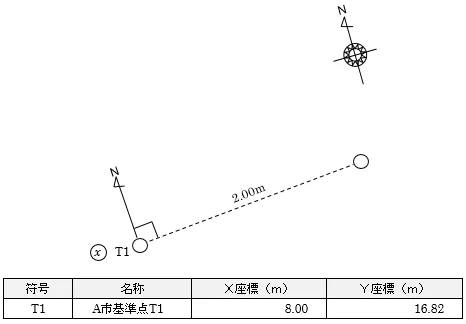
複素数の座標計算では,距離と方向角を指定して,移動後の座標を求めることができます。
↓こんな具合に。
①T1から90度方向に2.00m移動させた点の座標値を求める

どうですか?簡単そうでしょ??
まず,座標に数値を足すと,座標北(0°)の方向へ足したぶんだけ移動します。で,この数値の後に「∠」と角度を入力すると,移動に方向を与えることができるんです。
例題では座標北から90度の移動なんで,真横に移動することになります。なので,X座標に変化はありませんね。
答えは,X座標が8.00m,Y座標が18.82mとなります。
■点の移動(応用)
では,応用編として,T1からT2の方向に4.50m移動させた点の座標値を求めてみましょう。
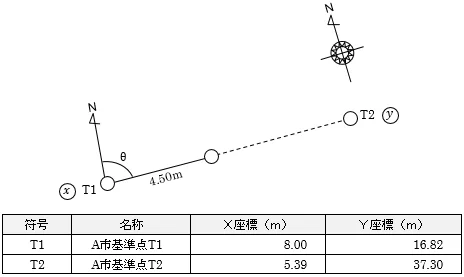
まずは,応用編の基礎として,方向角をメモリ「M」に記憶させて使用する方法でやってみましょう。
①T1からT2の方向角を求め,Mに記憶させる
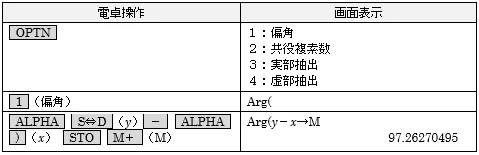
どうですか?記憶させる方法はマスターできましたでしょうか?
「=」の変わりに[ALPHA]して[メモリキー]です。
②T1からM方向に4.50m移動させた点の座標値を求める

そしたら,基礎編では「90°」と入れていたとこに「M」を入れてあげればOKです。
以上の計算により,T1からT2の方向に4.50m移動させた点の座標値は,計算結果の小数点以下第3位を四捨五入して,X座標が7.43m,Y座標が21.28mと求めることができました!
では,応用編の応用もやっときましょう。
さっきは方向角をメモリ「M」に記憶させて使用する方法でしたが,今度は[Ans]キーを使用した方法です。メモリを使わないので,色々と利点があります。
慣れたらこっちの方がいいですね。
①T1からT2の方向角を求める
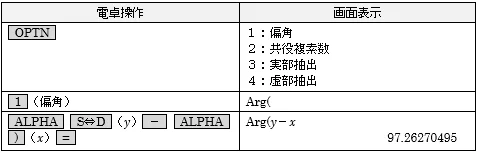
今度は記憶させません。普通に「=」を使ってください。
②T1から前の手順の答え方向に4.50m移動させた点の座標値を求める

そしたらさっきの「M」の変わりに[Ans]を使います。[Ans]には前の答え(≒97.26°)が記憶されてます。
手数に変化はありませんが,メモリを使わずに計算することができました!
[Ans]キーは使い慣れると非常に心強いので,ぜひ,このような工夫を上達に応じて取り入れてみてください。
本日はここまで!
次回は内分点をやります。よく調査士試験で出るやつですね。これも複素数だと驚くほど簡単に計算することができますよ!