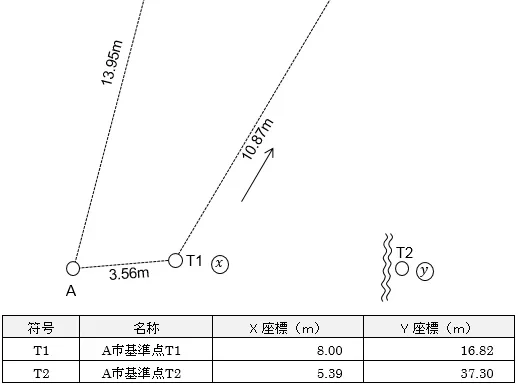
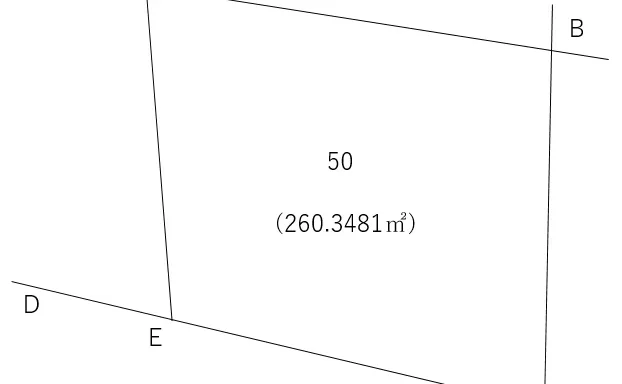
早くて正確に!複素数による測量計算ミニ講座㉑複合問題(座標間の平行移動・回転)
本ページにはプロモーションが
含まれていることがあります
今回は,応用的な問題として,座標間の平行移動・回転を複素数でやってみましょう。
平行移動は割と簡単ですが,回転となるとちょっと難しくなってきます。
みてみましょう。
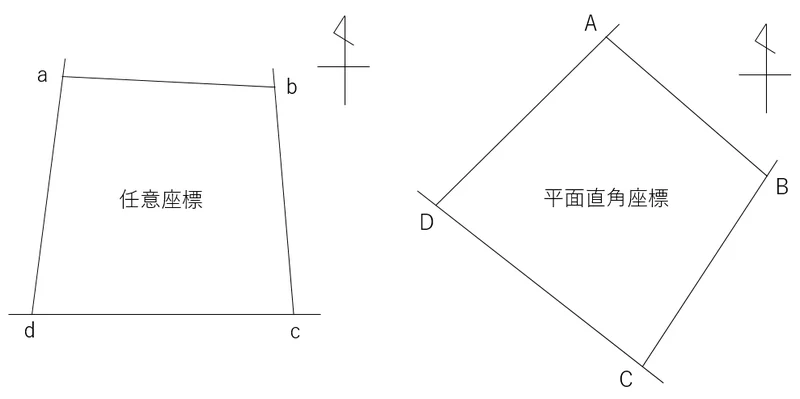
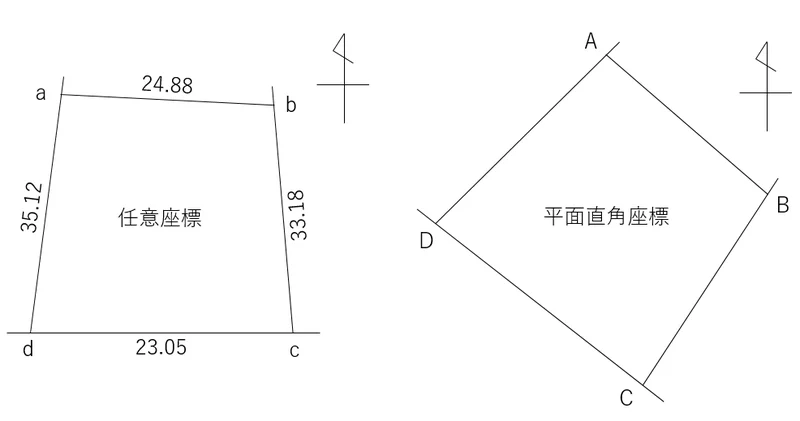
例えば,↓の図の左のような既存の地積測量図が当該地にあったとします。ですが,任意座標で観測されたものなので,平面直角座標系には乗りません。
<任意座標>
a X座標:155.28m Y座標:33.23m
b X座標:153.18m Y座標:58.02m
c X座標:120.22m Y座標:54.18m
d X座標:120.22m Y座標:31.13m
そこで,右のように基本三角点等からA点とC点を観測し,D点とB点の座標値を計算で求めることにしました。
<平面直角座標>
A X座標:-50173.13m Y座標:-14085.11m
C X座標:-50213.78m Y座標:-14081.11m
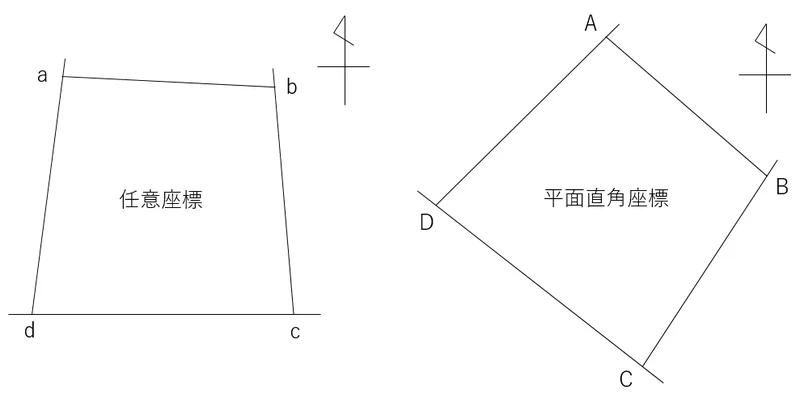
任意座標のa,b,c,dの各点は,それぞれ,平面直角座標のA,B,C,Dに相当します。
ところが,この両図の方位記号に注目してみてください。これらはそれぞれの「座標北」を示しているのですが,方位記号は同じ方向を向いているのに,当該地が回転しています。つまり,平行移動ではなく,座標が回転しているんですね。これを複素数で計算していきます。
回転していますが,各点の距離は正しいので,任意座標も以下のように点間距離を出すことができます。
あとは,B点とC点の座標は,A点とC点からの逆計算(2点からの距離が分かっている場合の計算)を使えば求めることができます。
でも,逆計算って慣れませんよね,第2余弦定理使うし。しかも2回やらないといけないので,計算量(打鍵数)が多いです。
そこで!
こういうときは「放射計算」を応用して解いてしまいましょう。放射計算なら,おなじみですし,1回で複数の点を回転・平行移動させることもできます!
まず,平面直角座標のうち,A点とC点は座標値が分かってます。なので,この2点を器械点と後視点にします。
この2点は,任意座標におけるa点とc点に相当します。なので,どちらでもいいのですが,今回は,a点を器械点に,c点を後視点として,b,d点の水平角と距離を計算します。
まずは,平面直角座標のA点とC点を,メモリAとCにストアし,任意座標のabcd各点をEFxyにそれぞれストアしましょう。忘れないように下の図のようにメモしておきます。

<任意座標>
a X座標:155.28m Y座標:33.23m →Eにストア
b X座標:153.18m Y座標:58.02m →Fにストア
c X座標:120.22m Y座標:54.18m →xにストア
d X座標:120.22m Y座標:31.13m →yにストア
<平面直角座標>
A X座標:-50173.13m Y座標:-14085.11m →Aにストア
C X座標:-50213.78m Y座標:-14081.11m →Cにストア
では,B点を求めてみましょう。ここでは,c点に器械を置いて,a点を後視とした放射計算でいきます。
まずは,距離。cb間の距離を求めて,Bにストアします。
Abs(F-x→B(33.1829…)
次に,a点を後視としたb点までの水平角を求めて,Mにストアします。
Arg(F-x=
Ans-Arg(E-x→M(37.5055…)
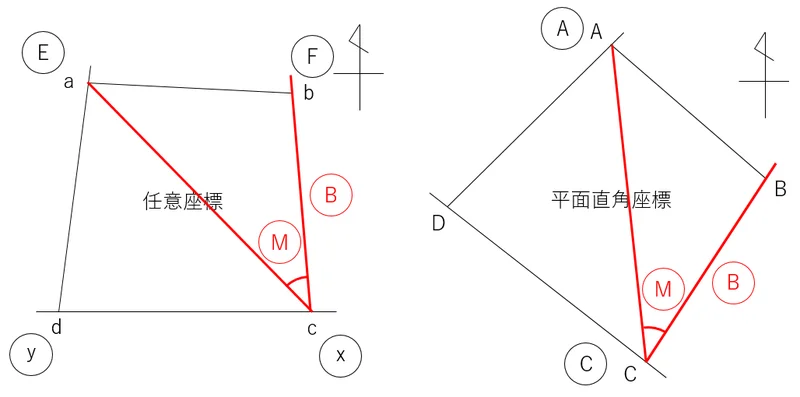
あとは,この水平角(M)と距離(B)を使って,A点を後視としたC点からの放射観測をしてあげれば,B点の座標値を求めることができます。
通常の放射計算と一緒ですね。
Arg(A-C=
C+B∠(Ans+M
これで,B点のX座標は-50185.60m,Y座標は-14063.58mと求めることができました。
同じように,D点も計算してみましょう!
X座標が-50203.95m,Y座標が-14101.96mとなれば正解です!
それでは!