＜お知らせ　2018.8.26追記＞

大変申し訳ありませんが，現在，kindle書籍のアップデートが当初の予定（７月）より大幅に遅れています。

アップデートが完了しましたら，こちらのブログにてご報告いたします。

よろしくおねがいします。

複素数ミニ講義の13回目です。

トラバース調整の理論編でお話したように，調査士試験ではトラバース調整の方法として，均等法（平成17年度）とコンパス法（平成20年度）両方の出題があります。

今回はコンパス法について解説します。

まだ見ていないという方は，トラバース調整（理論編）をご覧になってから本記事をお読みください。

また，末尾にkindle書籍のアップデート内容のお知らせもあります。

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

■コンパス法によるトラバ－ス調整

では，コンパス法によるトラバース調整を見てみましょう。

今回も問題を使って解説していきますが，前回の均等法と同じ例題を使って，E点をコンパス法で補正します。

ただし，「座標値の入力～放射計算を繰り返して閉合先の最後の観測点である「T1D」の座標値を算出するまで」についてはまったく同じなので省略します。前回の記事をご参照ください。

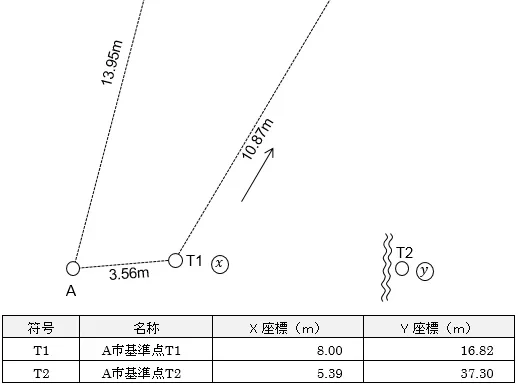
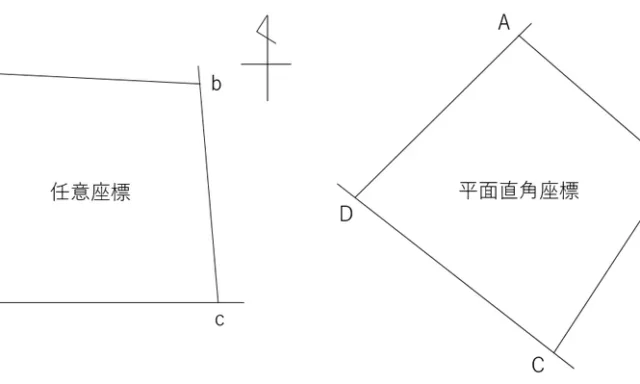
問題はこちら↓

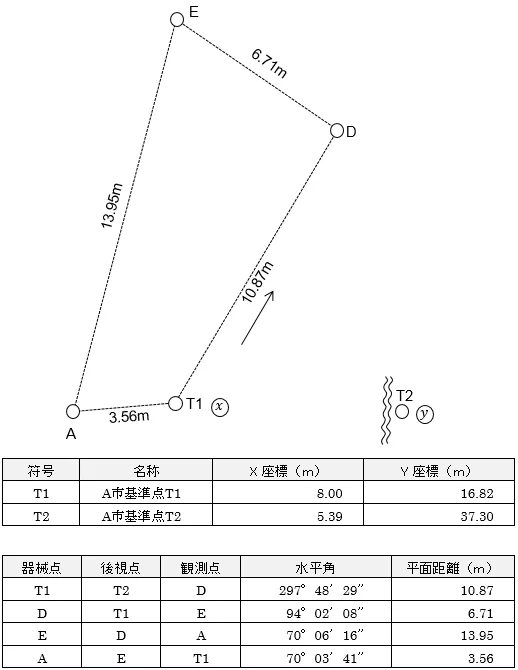
■補正量を算出する

ということで，いきなり補正量の算出にはいります。

ま，ここも前回と同じなんですが，大事なところなので繰り返します。

補正量とは，観測値に加えることで最確値となる数値です。なので，「正しい値」から「誤差を含んだ値」を引くことで計算することができます。

この場合では「T1－T1D」をすることで補正量を算出することができるってことですね。

⑦補正量を求める

正しく計算できていれば，「－9.18946952×10^(-4)　－8.511890425×10^(-3) i」と表示されるはずです。Ｘ方向に－0. 9mm，Ｙ方向に－8mmの最終的な補正量が出ていることとなります。

均等法では観測数で誤差を調整していきましたが，コンパス法では各辺長で調整することとなります。

つまり，補正量を観測辺長の合計で割って，それに観測点までの辺長の合計をかけて調整誤差を計算します。その調整誤差を観測結果に足すことで最確値を求めます。

では，実際に計算してみましょう。

観測辺長の合計は（10.87＋6.71＋13.95＋3.56）で，E点までの辺長は（10.87＋6.71）となります。

⑧コンパス法による閉合調整をし，Eに記憶させる

最後に，計算結果の小数点以下第３位を四捨五入し，E点の座標値は「X座標21.13ｍ，Y座標17.85ｍ」と求めることができます。

この例題では結果が均等法と一緒でした。

補正量（－∆β）は誤差（∆β）を調整するためのものなので，元の観測値に足すということに注意してください。

以上です！
どうでしたでしょうか？考え方・理論さえしっかり押えておけば簡単ですね！ところが過去問で出題されているにも関わらず，対策を怠っている受験生がいるのも事実です！差をつけましょう！！

さて，次回のミニ講座ですが，結構この複素数ミニ講座をはじめてから，メールやコメントにてkindle読者の方からメッセージを頂くようになりました。kindleの方は７月に大幅なアップデートを予定しています。購入済みの方は無料でアップデートされますよ。

ちなみに，kindle書籍ってのはコレ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

で，そのアップデート内容の一端を先取りして記事にします。まずは「逆計算」です。

ちなみに，アップデート内容は以下のとおりです。

kindle読者の方なら「おっ」と思う内容ではないでしょうか？

＜追加＞

・関数の説明

・点の移動

・逆計算

＜応用＞

・もっと早くて簡単な求積方法（四角形限定）

・メモを使わない交点計算

・セットバックの交点計算

＜修正・変更＞

・四捨五入のタイミング

・使用する電卓（fx-JP500）

・本試験形式の練習問題

・一部カラー化（予定）

それでは！