複素数ミニ講義の12回目です。

前回はトラバース調整の理論編でしたので，今回は実戦編として均等法による調整を解説いたします！

前回，理論編とはいえ，中身にまで踏み込んでいますので，まだ見ていないという方は是非，そちらの記事をご覧になってから本記事をお読みください。

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

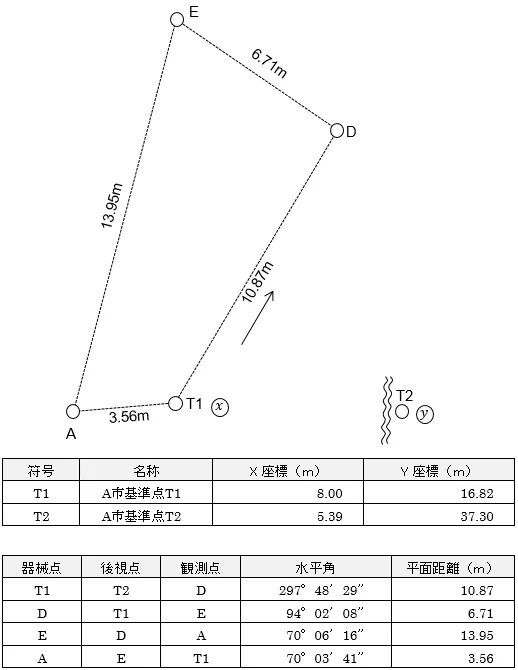
■均等法によるトラバ－ス調整

ここでは閉合トラバースの均等法による補正計算を解説します。
閉合でも結合でも同じ考えになります。

では，実際に閉合トラバ－スで観測したE点を均等法で補正していきましょう。

問題はこちら↓

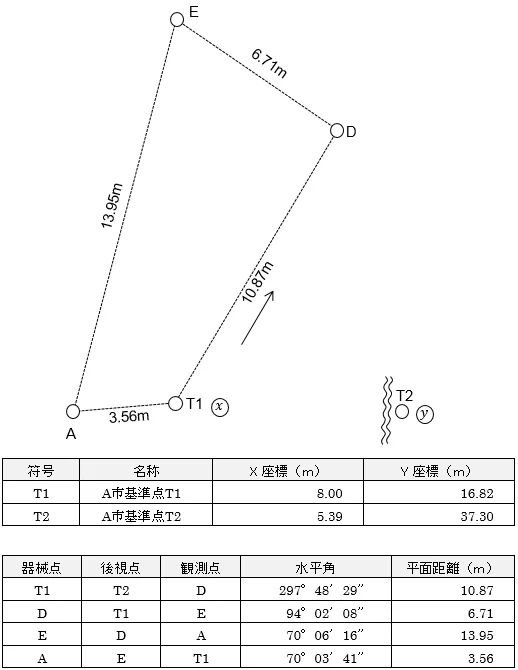
■座標値の入力

まずは，既知点であるT1とT2をそれぞれメモリに記憶させましょう。
今回もT1を「x」に，T2を「y」に記憶させます。

①T1をxに記憶させる

②T2をyに記憶させる

■放射計算

前々回の記事である放射計算の繰り返しになりますが，D点の座標値を計算しましょう。
今回はD点をメモリ「Ｄ」に記憶させますが，一手で計算してみます。

③T1からT2の方向角を求め，方向角と距離でD点の座標を出し，Dに記憶させる

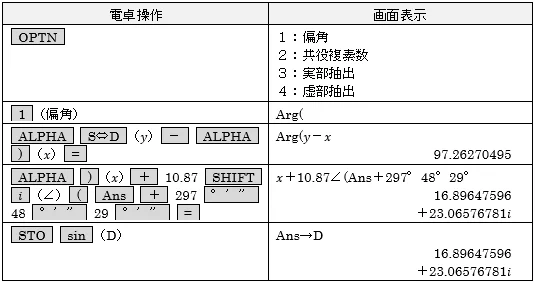
続けて，E点とA点，さらにT1まで連続して計算しましょう。
放射計算を繰り返す感じですね。
閉合先の最後の観測点であるT1は，「x」に入力したものと混同させないよう，「T1D」と呼ぶこととしましょう。
E点は「E」に，A点は「A」に記憶させ，最後のT1Dは入力したものと混同しないよう，「M」に記憶させます。特に新しい操作はありませんね。

④DからT1を後視にし，方向角と距離でE点の座標を出し，Eに記憶させる

⑤EからDを後視にし，方向角と距離でA点の座標を出し，Aに記憶させる

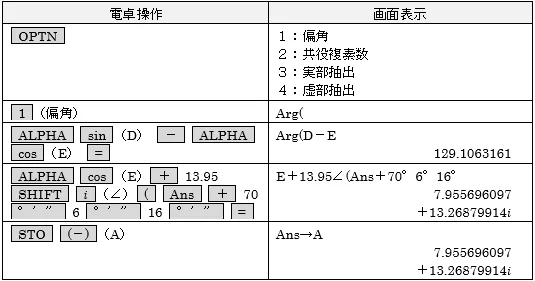
⑥AからEを後視にし，方向角と距離でT1Dの座標を出し，Mに記憶させる

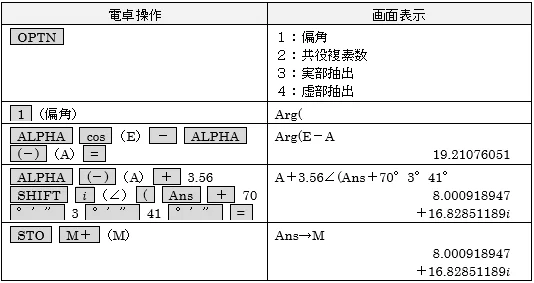
放射計算が続きましたね。これでT1Dの座標値が算出できました。
このT1Dの座標値と，既知のT1の座標値の差が誤差の補正量となります。


■補正量を算出する

前回の記事でお話しましたが，補正量とは，観測値に加えることで最確値となる数値です。
なので，「正しい値」から「誤差を含んだ値」を引くことで計算することができます。この場合では「T1－T1D」をすることで補正量を算出することができるってことですね。

⑦補正量を求める

正しく計算できていれば，「－9.18946952×10^(-4)　－8.511890425×10^(-3) i」と表示されるはずです。
大事なのでもう一回いいます。補正量は「正しい値」から「誤差を含んだ値」を引くことで計算できます。「正引く誤が補正量」。この「正引く誤」という順番は非常に重要です。もし逆に引いてしまうと誤差を逆に増幅させる結果となってしまいます。しっかり覚えましょう！！！

さて，「－9.18946952×10^(-4)　－8.511890425×10^(-3) i」ってことは，Ｘ方向に－0. 9mm，Ｙ方向に－8mmの最終的な補正量が出ていることとなります。これを分散し，各観測結果に足していくことで，誤差を調整した最確値を求めることになります。

今回は均等法で誤差を調整することになるので，この補正量を観測数で割って，観測結果に観測数分足していきます。
T1からT1Dを求めるまでの観測数は４回，そして，求めるべき「E」までの観測数は２回です。

では，実際に補正してみましょう。

⑧均等法による閉合調整をし，Eに記憶させる

できましたか？？
最後に，計算結果の小数点以下第３位を四捨五入し，E点の座標値は「X座標21.13ｍ，Y座標17.85ｍ」と求めることができました。
測量計算に限らず，補正量（－∆β）は誤差（∆β）を調整するためのものなので，元の観測値に足すことで最確値を算出します。


それでは！次回はコンパス法によるトラバ－ス調整をやってみましょう！