ＧＷ終わりました！本試験までラストスパートです！
ミニ講座４回目，本日は「機器の点検」，「水平角の観測」，「鉛直角の観測」です。
 

▼動画です！

■機器の点検

測量の機械は事前に検定や点検調整をしなければなりません。精度が出ませんからね。
トータルステーション（以下，ＴＳ）もしかり。
測量士補試験で押さえる機器の点検は「三点法」です。

三点法とは，距離の観測精度を点検するための簡便な点検法です。
ずっと出題がなく，いきなりH29測量士補試験で出ましたが，過去には頻出の問題です。

どういった点検法かというと，これはＴＳの距離の補正値（器械定数と反射鏡定数の和）を求めるものです。
図のように，平たんな土地にＡ，Ｂ，Ｃを一直線上に設けて，ＡＢ，ＢＣ，ＡＣの距離を測定し，図中の計算をすることで，器械定数と反射鏡定数の和を求めることができます。
で，この補正値をＡＣの距離に加えることで，距離が補正されます。

なんで？というと，器械定数と反射鏡定数の和というのは距離に関わらず発生するんです。なので，ＡＢでもＢＣでもＡＣでも等しく発生します。

ＡＢとＢＣの和には２つ分，これをＡＣ（１つ分）から引くので，マイナス１つ分が補正値になります。これをＡＣの距離に足せば，距離が補正されるわけですね。

機器の点検としては三点法を押さえておけば大丈夫です。

■水平角の観測

いよいよ「観測」の工程に入っていきます。
（前回の作業工程をみてください。これに沿ってミニ講座は進めていきます。）

観測の工程では，平均図などに基づき関係する点間の水平角，鉛直角，距離などの観測をしていきます。
現地で観測をおこなう前に，測量計画機関から承認を得た平均図に基づき，効率的な観測をおこなうための【観測図】を作成します。観測図の作成においては，点検計算がおこなえるよう配慮する必要もあります。

まずは，水平角の観測です。

角度（水平角）の観測では，観測時に「手簿」という測量ノートにメモしていきます。メモした値から観測差・倍角差を計算で求めると，その場で観測精度の確認ができるようになっています。ちなみに１級基準点測量では倍角差15″，観測差8″までという制限があり，超えるようだったら，「再測！やり直し！」となっちゃうわけですね。

手簿は↓こんな感じ。

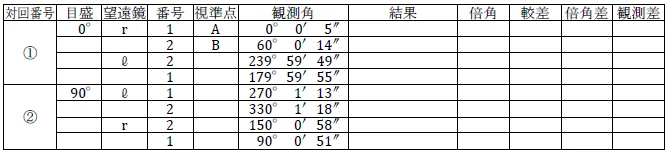
では，この観測手簿の測量の内容はどうなっているのか？
順を追って書いていきます。

　① トータルステーションを整置する。
　② 水平目盛を0°付近にし，基準となる点Aを視準し，目盛（0°0′5″）を読む。
　③ 新点である点Bを視準し，目盛（60°0′14″）を読む。
　④ 望遠鏡を180°反転させる。②③の観測が正（r），⑤⑥の観測が反（ℓ）となる。
　⑤ 正の観測とは逆に，反の観測では点Bから視準し，目盛（239°59′49″）を読む。
　⑥ 基準となる点Aを視準し，目盛（179°59′55″）を読む。
　⑦ ２対回測量をする場合，水平目盛を90°付近にし，もう一度基準点となる点Aを視準し，目盛（270°1′13″）を読む。
　⑧ 新点である点Bを視準し，目盛（330°1′18″）を読む。
　⑨ 望遠鏡を180°反転させる。２対回目では，⑦⑧の観測が反（ℓ），⑩⑪の観測が正（r）となる。
　⑩ 点Bを視準し，目盛（150°0′58″）を読む。
　⑪ 点Aを視準し，目盛（90°0′51″）を読み，観測は終了。

手簿の数値を見ながら，観測の様子をイメージしてみてください。
ちなみに，２対回目の目盛が90°から始めるのは，目盛誤差（目盛盤の目盛間隔が均等でないことで生じる誤差）を軽減するための観測工夫です。

で，前述した観測差・倍角差を計算で求めて，現地で観測精度を確認します。
現地で確認できることに意味があるんですね，事務所に帰ってからやり直しじゃ効率的じゃないので。

下が現地計算をおこなった手簿です。

　① 新点（B）の観測角から基準となる点（A）の観測角を引いて，結果（水平角）を計算する。例えば，１対回目の正観測Bの結果は，60°0′14″－0°0′5″＝60°0′9″となり，２対回目の正観測Bの結果は，150°0′58″－90°0′51″＝60°0′7″となる。
　② 対回ごとに，新点の結果について正反の合計を計算する。この値を倍角という。通常は度分秒すべてを合計する必要はなく，秒の単位だけ合計すれば足りる。ただし，この観測例がそうであるように，分の単位の数字が異なる場合，もっとも小さいものを基準とする。この観測では，１対回目の反の結果が59°59′54″であるため，他の値も「59°59′」に合わせ，秒の数字に60を足して考える。１対回目の倍角は69″＋54″＝123″となり，２対回目の倍角は65″＋67″＝132″となる。
　③ 新点の結果について正の結果から反の結果を引く。この値を較差という。結果は変わらないが，分の単位の数字を合わせた上で秒の単位だけ計算すればよい。１対回目の較差は69″－54″＝＋15″となり，２対回目の較差は67″－65″＝＋2″となる。
　④ 倍角の最大値から最小値を引く。この値が倍角差となる。この観測では，132″－123″＝9″が倍角差となる。
　⑤ 較差の最大値から最小値を引く。この値が観測差となる。この観測では，＋15″－（＋2″）＝13″が観測差となる。
　⑥ 倍角差と観測差の両方が許容範囲内であれば，２対回分の結果を平均したもの（４回分の合計÷4）を最確値とする。観測例が１級基準点測量であった場合，許容範囲は倍角差15″，観測差8″までのため，観測差が許容範囲を超えており，再測を要することになる。

ちょっと長いのですが，現地計算の内容は↑こんな感じ。
かなり情報を詰め込んだので読みづらいのが恐縮ですが，お手持ちのテキストや過去問集と見比べてみてください。ちょっとでも理解の助けになればと思います。

■鉛直角の観測

ＴＳでのでの基準点測量では，水平角および鉛直角の観測と距離の測定は１視準で同時に行われます。
水平角観測の必要対回数（２対回）に合わせて，取得された鉛直角の観測値をすべて採用し，その平均値を最確値とすることができるようになっています。

１　高低角

注意しなければならないのが，ＴＳで観測される鉛直角とは，天頂（真上）から目標に対する角度のこと！計算をすることで高低角を出さなければなりません。

図をみてください。

観測できるのは天頂から目標までの「鉛直角」。知りたいのは「高低角」です。
高低角とは，水平線を基準とした目標に対する角度のことで，水平線よりも上（目標が器械よりも高い位置にある）であれば＋の符号になり，水平線よりも下（目標が器械よりも低い位置にある）であれば－の符合になります。なので，90°－鉛直角＝高低角と計算することができます。

２　高度定数

鉛直角の観測でも，観測精度をみるための計算があります。それが「高度定数の較差（こうさ）」です。
高度定数とは，「鉛直観測における正反観測の誤差」のこと。
本来だったら，望遠鏡の正反の観測値を合計すると360°になるはずです。でも，実際には器械固有の誤差がどうしてもあり，360°にはなりません。この差が,（つまり，望遠鏡の正反の観測値の合計－360°）が高度定数です。

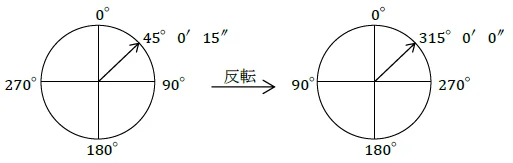
上の図で言えば，正反の観測値の合計は本来360°になるべきなのに，360°0′15″となっています。
ですので，高度定数は15″。
この高度定数のばらつきをみたのが高度定数の較差であり，一連の観測における高度定数の最大値と最小値の差を高度定数の較差といいます。

３　間接水準測量

さて，高さの観測でもう１つ大事なのがあります。それが間接水準測量の計算問題。

普通，水準（高さ）を観測する場合はレベルを使った水準測量をします。でも，ＴＳを使って，たくさんの点の高さを観測することができます。ちょっと精度は悪いんですけどね。これを間接水準測量といいます。（ちなみに，レベルを使った水準測量を直接水準測量といいます。）

下のような計算問題が出題されます。



まぁ問題文の値を足したり引いたりしていけば答えは出るんですが，やっかいなのが「両差」です。
地球は球面であるため，観測距離が長くなる間接水準測量では，この影響を考慮する必要があります。球面であることによる誤差のことを球差といい，大気の屈折による誤差である気差とあわせて「両差」といいます。
両差の影響により，間接水準測量では目標が実際よりも低く観測されるわけですが，この両差を計算結果から足すのか？引くのか？これが迷いどころです。

では，ポイントを押さえておきましょう。

まず，間接水準測量には３パターンあります。

①既知点（高さが分かっている点）に器械を整置し，新点（高さを知りたい点）を観測する「正方向」
②新点（高さを知りたい点）に器械を整置し，既知点（高さが分かっている点）を観測する「反方向」
③既知点と新点で同時に観測を行う「同時観測」

それぞれ，両差を①なら足す。②なら引く。③は無視。
問題は大部分が①の正方向ですが，②と③も出題履歴がありますので，要注意です。


次回は作業工程に沿って「多角計算」と「点検計算」，「成果等の整理」をやります。これで「多角測量」の分野が終わります。

▲まとめ に戻る！▲