複素数ミニ講義の７回目です。

今回は，「内分点」です。

内分点とは，「ある点とある点の間をＰ：Ｑで分割したい場合」に使用する計算方法です。

考え方によっては前回の点の移動なんですが，複素数を使うと，とても早く計算することができます！

ちなみにこの内分計算，調査士試験で頻出です。

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

■内分点

さて，今回も演習っぽい形式でやってみましょう。
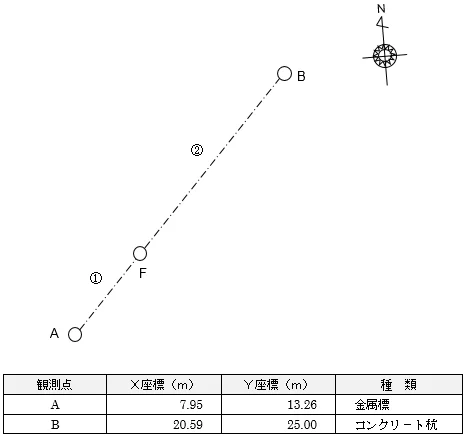
下の図のA点とB点を１：２で内分するF点を求めます。

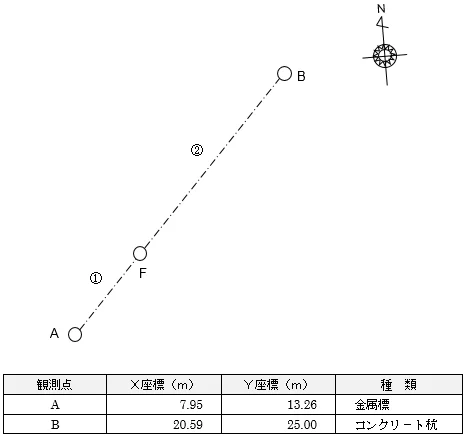
ちなみに，点の移動でやる場合，「AからBまでの方向角を求めて，その方向にAからBまでの点間距離の1/3の距離を伸ばした点を求める」という方法を取ることになります。

是非，こちらの方法も考えてやってみてください。

では，複素数ではどうやるのか？
これも複素数の「X座標とY座標が１つの数値となっている」特徴を上手く使ったやり方です。

まずは，A点を「A」，B点を「B」にそれぞれ記憶させます。

①A点をAに記憶させる

②B点をBに記憶させる

それでは具体的なやり方ですが，方法を言葉で説明するとこうなります。
「BとAの差の1/3を出して，それをAに加える」
イメージとしては下の図のような感じですね。

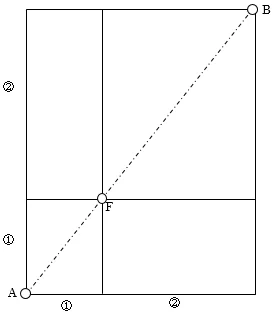
やってみましょう。
まずは，BとAの差を求めます。

①BとAの差を求める

で，この①の答えの1/3をAに加えれば完成です。

②前の手順の答えの1/3をAに加える

どうでしょうか？

[Ans]キーを上手く使ってます。こういうところがスッとできれば上達者。

計算結果の小数点以下第３位を四捨五入し，F点の座標値はX座標12.16ｍ，Y座標17.17ｍとなります。
普通の計算だと，X座標とY座標ごとに比例の計算をしなければならないので，ここだけ切り取っても２倍早く計算できるわけですね。
こういうのが積み重なると大きな差がでます。

では次回は「鬼門」である交点計算をやりましょう！