前回は，指定面積の座標値の出し方に，「交点計算」を使いました。
これはこれで万能（セットバックに使える）なんですが，ここでは同じ問題を「内分点」を使って解く方法を紹介します。
計算分量的には今回の方が有利ですね。爆速です。

三角形CAEの面積を求めるところまでは同じですが，ページを行ったり来たりするのは面倒ですので，最初から繰り返します。

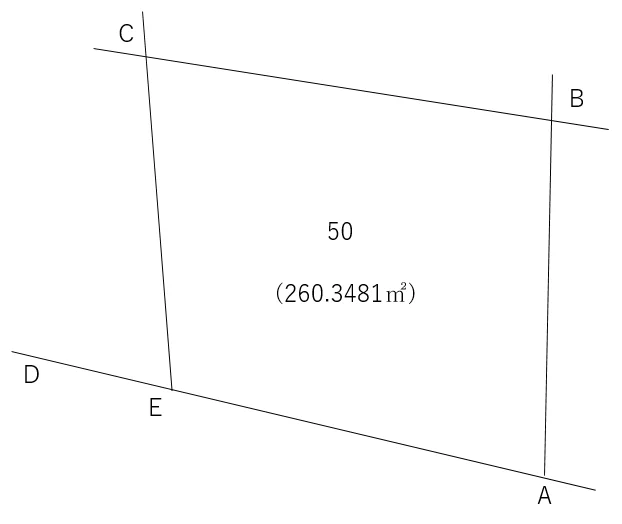
問：下の土地の地積が【260.3481㎡】になるＥ点の座標値を求めてください。
　　Ｅ点は直線ＤＡ上にあります。

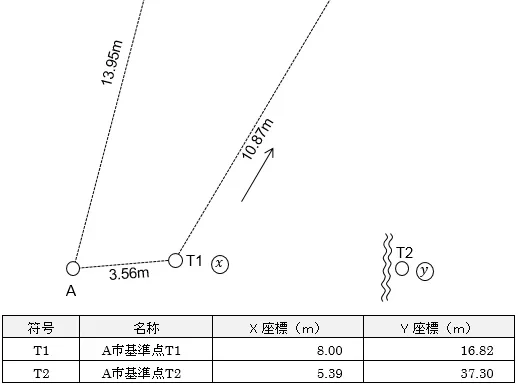
座標値は，以下の通りです。点名，Ｘ座標，Ｙ座標の順。

Ａ　40.00　52.00
Ｂ　56.73　54.14
Ｃ　60.00　35.00
Ｄ　41.80　38.47

これらは計算に使いますので，電卓のメモリに記憶（ストア）させておきます。
点名と同じメモリに記憶させておけば，ミスを防げます。

40＋52 i → Ａ
56.73＋54.14 i → Ｂ
60＋35 i → Ｃ
41.8＋38.47 i → Ｄ

まず，Ａ，Ｂ，Ｃの各点の座標値は既知ですので，面積を求めることができます。
出してみましょう。

Conjg（Ｃ）Ｂ＋Conjg（Ｂ）Ａ＋Conjg（Ａ）Ｃ＝
Ans÷2＝
Imp（Ans＝（163.605）

これで，三角形CBAの面積が163.605㎡と求まったので，当該土地の地積（260.3481㎡）から引くことで，座標値が不明なＥ点を含んだ三角形CAEの面積を求めることができます。あとで使うので「ｘ」に記憶させておきましょう。

260.3481－Ans → ｘ（96.7431）

次に，既知のＣ，Ａ，Ｄの各点で構成される三角形CADに注目します。
三角形CADの面積を以下の計算で求めます。あとで使うので「ｙ」に記憶させておきましょう。

Conjg（Ｃ）Ａ＋Conjg（Ａ）Ｄ＋Conjg（Ｄ）Ｃ＝
Ans÷2＝Imp（Ans → ｙ（120）

これで，三角形CADの面積が120㎡であると求まりました。次の図をみてください。

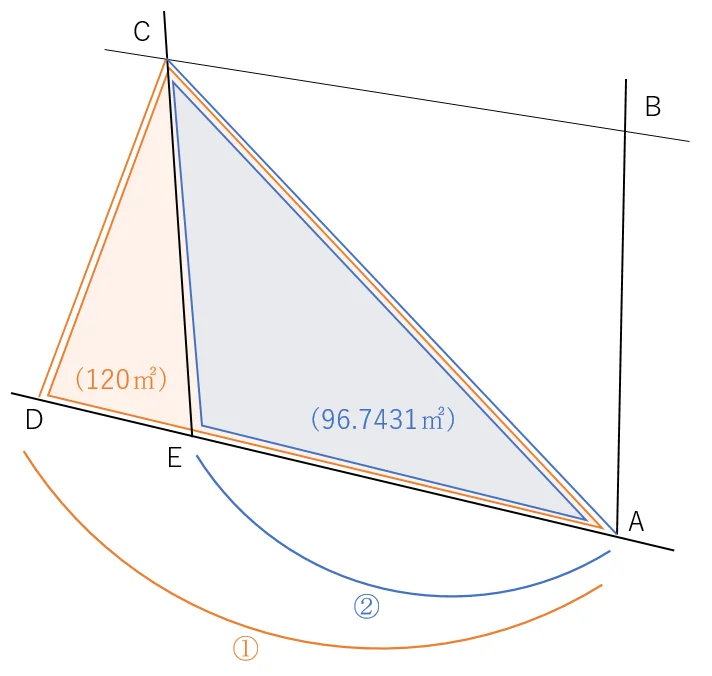
「三角形CADの面積」と「三角形CBAの面積」の比は，（高さが共通の三角形ですので）図中の距離DA（①）と距離EA（②）の比となります。
そのため，面積の比で直線DAを内分してあげることで，Ｅ点の座標値を求めることができます。Ｅ点の座標値は「Ｅ」に記憶させます。
やってみましょう。

Ｄ－Ａ＝
Ans÷ｙ×ｘ＝
Ans＋Ａ → Ｅ（41.451…＋41.092… i ）

はい！
ということで，Ｅ点の座標値は，小数点以下第３位を四捨五入して，Ｘ座標「41.45ｍ」，Y「41.09ｍ」となれば正解です！
（当たり前ですが，前回の記事の答えと同じです。）
できましたか？


それでは！