ちょっと前回の記事が好評でしたので，他所で質問がきた内容を複合問題にしました。
セットバックなどにも使える，交点計算の応用問題です。

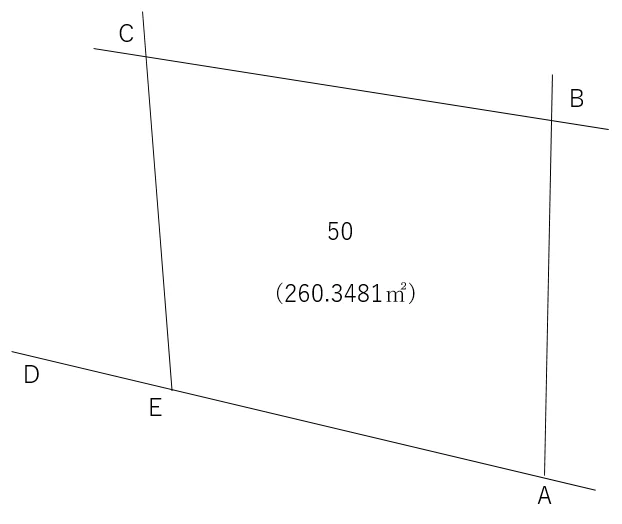
問：下の土地の地積が【260.3481㎡】になるＥ点の座標値を求めてください。
　　Ｅ点は直線ＤＡ上にあります。

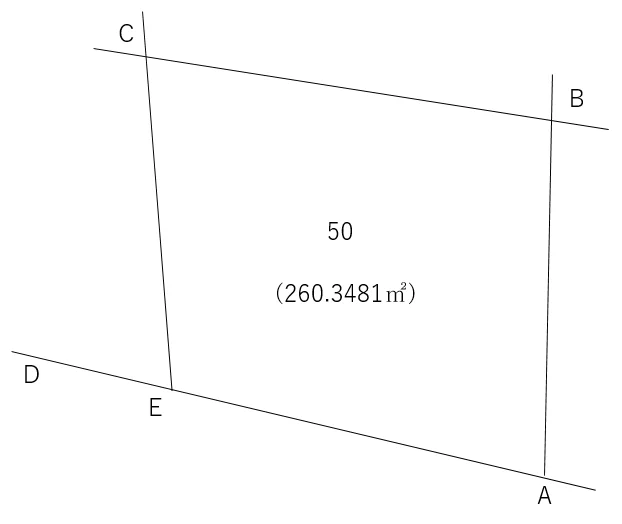
座標値は，以下の通りです。点名，Ｘ座標，Ｙ座標の順。

Ａ　40.00　52.00
Ｂ　56.73　54.14
Ｃ　60.00　35.00
Ｄ　41.80　38.47

これらは計算に使いますので，電卓のメモリに記憶（ストア）させておきます。
点名と同じメモリに記憶させておけば，ミスを防げます。
 

40＋52 i → Ａ
56.73＋54.14 i → Ｂ
60＋35 i → Ｃ
41.8＋38.47 i → Ｄ

まず，Ａ，Ｂ，Ｃの各点の座標値は既知ですので，面積を求めることができます。
出してみましょう。
 

Conjg（Ｃ）Ｂ＋Conjg（Ｂ）Ａ＋Conjg（Ａ）Ｃ＝
Ans÷2＝
Imp（Ans＝（163.605）

これで，三角形CBAの面積が163.605㎡と求まったので，当該土地の地積（260.3481㎡）から引くことで，座標値が不明なＥ点を含んだ三角形CAEの面積を求めることができます。あとで使うので「Ｍ」に記憶させておきましょう。
 

260.3481－Ans → Ｍ（96.7431）

三角形の面積は，「底辺×高さ÷２」です。
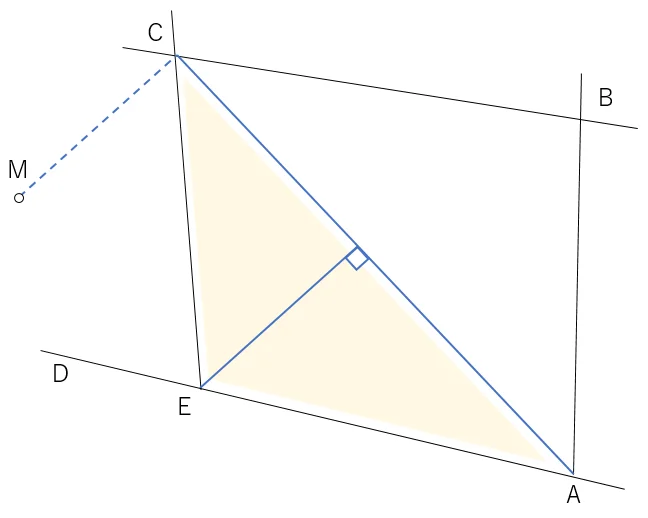
三角形CAEの底辺をCA（こちらは点間距離で出せますね）とすると，以下の図のようになります。

では，底辺をＣ点Ａ点の点間距離で求め，高さｙを求めてみます。これも後で使うので，「Ｍ」に上書きしましょう。
 

Abs（Ｃ－Ａ＝
Ｍ×2÷Ans → Ｍ（7.371…）

これで高さが求まりました。
あとは，セットバックのような計算をすればOKです。
まずは，Ｃ点から，Ａ点の方向角＋90°の方向に，三角形の高さ（Ｍ）分移動した点を仮に「Ｍ点」として作成します。図にするとこんな位置ですね。

計算してみましょう。
 

Arg（Ａ－Ｃ＝
Ｃ＋Ｍ∠（Ans＋90 → Ｍ（55.2260…＋29.3835… i ）

あとは，このＭ点を使った交点計算をすれば終わりです。
Ｍ点から交点Ｅまでの方向角（ｘ）は，Ｃ点からＡ点までの方向角と同じです。

Ｃ点からＡ点までの方向角を計算して，「ｘ」に記憶させましょう。

Arg（Ａ－Ｃ → ｘ（139.635…）

同じように，Ａ点からＤ点までの方向角（ｙ）を計算して，「ｙ」に記憶させます。

Arg（Ｄ－Ａ → ｙ（－82.422…）

これで２つの方向角がそろいました。
あとは，交点計算の方法でＥ点の座標値を求めるだけです。
実部抽出を使って，Ｅ点の座標値は「Ｅ」に記憶させます。

tan(ｘ)＋ i → ｘ
tan(ｙ)＋ i → ｙ
Ｍｘ－Ａｙ＝
Ans÷（ｘ－ｙ＝
Rep（Ans → Ｅ
Ans－Ｍ＝
Ans×ｘ＝
Rep（Ans) i ＋Ｅ → Ｅ（41.451…＋41.092… i ）

はい！
ということで，Ｅ点の座標値は，小数点以下第３位を四捨五入して，Ｘ座標「41.45ｍ」，Y「41.09ｍ」となれば正解です！
できましたか？


それでは！