このブログでは中山式複素数の各論は記事にしたことがありますが，それらを組み合わせた問題をやってみましょう。

内分や交点計算を含んだ複合的な問題です。これができれば身についています！

問：下の土地のＦ点の座標値を求めてください。

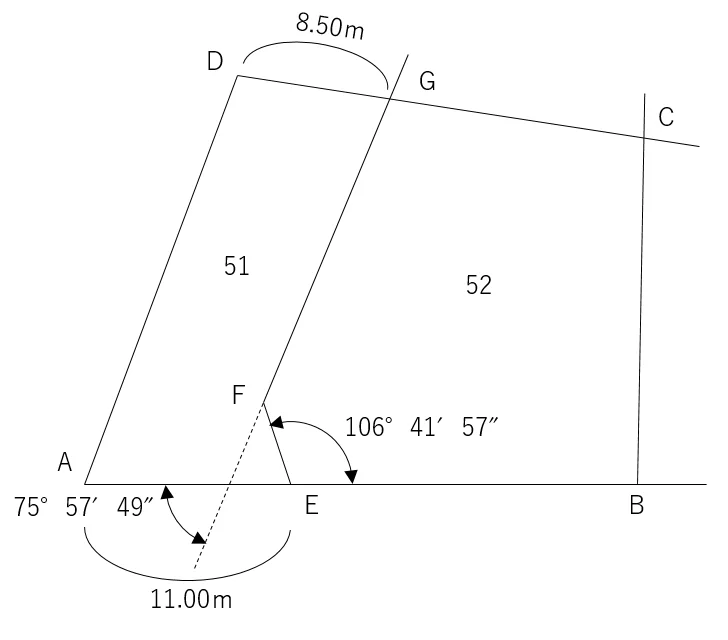
座標値は，以下の通りです。点名，Ｘ座標，Ｙ座標の順。

Ａ　40.00　30.00

Ｂ　40.00　52.00

Ｃ　56.73　54.14

Ｄ　60.00　35.00

これらは計算に使いますので，電卓のメモリに記憶（ストア）させておきます。

点名と同じメモリに記憶させておけば，ミスを防げます。

40＋30 i → Ａ

40＋52 i → Ｂ

56.73＋54.14 i → Ｃ

60＋35 i → Ｄ

まず，Ｅ点とＧ点の座標値が分かりませんから，これを求めます。

Ｅ点は，Ａ点からＢ点の方向角（座標北から右回りの角度）に，11ｍ進んだ点です。

点の移動で求めます。

Arg（ Ｂ－Ａ＝

Ａ＋11∠Ans → Ｅ （40＋41 i ）

Ｅ点の座標値は「Ｅ」に記憶させました。

次に，Ｇ点の座標値を求めます。

Ｇ点は，Ｄ点からＣ点の方向角に，8.5ｍ進んだ点です。

Arg（C－Ｄ＝

Ｄ＋8.5∠Ans→Ｍ （58.568…＋43.378… i ）

Ｇ点の座標値は「Ｍ」に記憶させました。

あとは，Ｅ点とＧ点の交点計算でＦ点の座標値を求めることができます。

交点計算をする際には，Ｅ点からＦ点まで，と，Ｇ点からＦ点まで，の２つの方向角が必要です。

Ｅ点からＦ点までの方向角（ｘ）は，Ａ点からＢ点までの方向角から，106°41′57″を引いたものです。

方向角は「右回り」なので，左回りに角度を回すときは引きます。

Ｅ点からＦ点までの方向角を計算して，「ｘ」に記憶させましょう。

Arg（ Ｂ－Ａ＝

Ans－106°41°57°→ ｘ（－16.699…）

同じように，Ｇ点からＦ点までの方向角（ｙ）を求めます。

Ｇ点からＦ点までの方向角は，Ｂ点からＡ点までの方向角から，75°57′49″を引いたものです。

Arg（ Ａ－Ｂ＝

Ans－75°57°49°→ ｙ（－165.963…）

これで２つの方向角がそろいました。

あとは，交点計算の方法でＦ点の座標値を求めるだけです。

実部抽出を使って，Ｆ点の座標値は「Ｆ」に記憶させます。

tan( ｘ )＋ i → ｘ

tan( ｙ )＋ i → ｙ

Ｅｘ－Ｍｙ＝

Ans÷（ ｘ－ｙ＝

Rep（ Ans → Ｆ

Ans－Ｅ＝

Ans×ｘ ＝

Rep（ Ans ) i ＋Ｆ→ Ｆ （44.115…＋39.765… i ）

はい！

ということで，Ｆ点の座標値は，小数点以下第３位を四捨五入して，Ｘ座標「44.12ｍ」，Y「39.77ｍ」となれば正解です！

できましたか？

それでは！