複素数ミニ講義の17回目です。

それでは，四角形の土地に限定した「簡易な求積計算」について解説いたします。

もちろん，四角形の土地であっても前回の方法で求積することができますが，こちらのやり方の方が，簡単で早いですよ。

今回も，四捨五入のタイミングなど非常に大事なことが含まれている，面積計算「大事なこと編」を是非ご一読ください！！

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

それでは，簡易な方法でも，前回と同じ土地（２番３）を求積します。
問題は同じですが，こちら↓

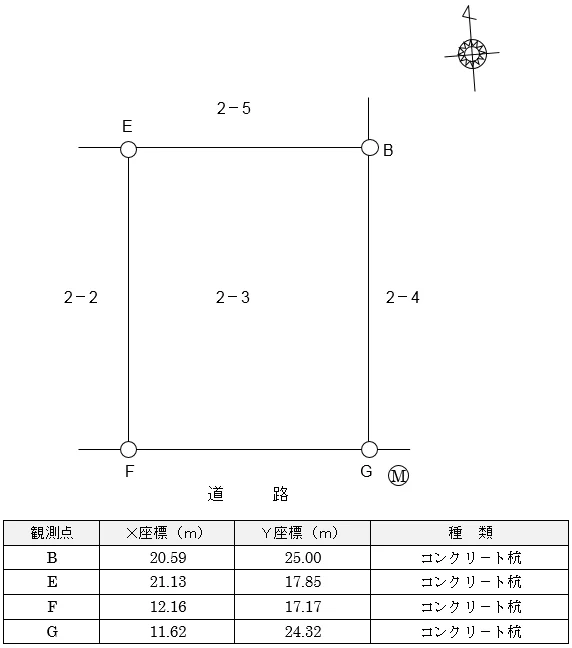
■座標値の入力

前回の基本編と同様，土地を構成する点をすべてメモリに入力します。

B，E，F及びGの各点がそれぞれ「B」，「E」，「F」及び「M」に記憶させますが，前回と同じですのでスキップします。


■簡易な求積

この簡易な方法でも，共役複素数である「Conjg」関数を使用します。
計算結果の虚部（下の段）が倍面積となるのも同じです。

計算方法だけが違うってことですね。

通常の方法では構成点の１点から時計回りに入力しましたが，簡易な方法では以下のように「たすきがけ」で入力していくことになります。

実際に見た方が早いですね！やってみましょう。

どうでしょう？？
なんだか前回の求積は長くて複雑そう（実際やってみれば単なる繰り返しなので，そんなに複雑じゃないんですが…。）なんですが，こっちは簡単そうですね！実際，簡単ですよ！！

「Conjg」関数のかっこの中に，たすきがけ①の順に座標値を引きます。で，これをかっこでくくって，たすきがけ②の順に座標値を引いたものをかけてあげればOKです。

「Conjg」関数を１度しか使用しないため，一般的な求積方法よりも圧倒的に早いです。前回の電卓の表示と比べてみてください。同じ土地ですからね。
ちなみに，たすきがけの形で座標を引けば，その順番に決まりはありません。②からやっても同じ結果になります。

正しく計算できていれば，画面表示のとおり「64.5027㎡」となり，当たり前ですが，通常の求積方法による計算結果と同じ答えが出ます。


はい！
長かったんですが，これで複素数のミニ講座が終了です！
他にも辺長の計算とか，一連の流れとか…やりたいことはたくさんあるんですが，全部やっちゃうとkindleとかアガルートの講座が意味なくなっちゃうので，これにて終了です。ごめんなさい。

「肝」の部分は全部ミニ講座で触れたので，「この先」については，kindleやアガルートの講座にて，またお会いしましょう！「複素数って早いな」と少しでも感じていただければ良かったです。

それでは！