複素数ミニ講義の11回目です。

今回はトラバース調整の「理論」をやります。

で，次回から，実戦編として，「均等法」と「コンパス法」をそれぞれやっていく予定です。

ちなみに調査士試験では，トラバース調整の「均等法」と「コンパス法」，どちらも出題されたことがあります。

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

■トラバース調整とは？

測量には誤差がつきものです。
測量士補でやったように，消去・軽減できる誤差はもちろん潰していくんですが，どうしても誤差は残ってしまうんですね。なので，測量では真値を観測することはできません。なので，いろいろ工夫をして，最も確からしい値，「最確値」を求めていくわけです。

その工夫の１つがトラバース調整です。
下の図をみてください。

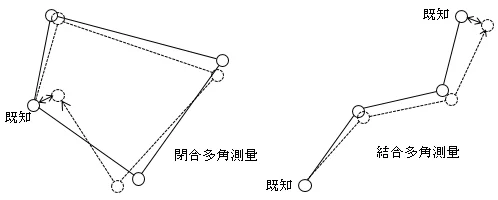
左が閉合多角測量で，右が結合多角測量です。

どちらも順々に既知点（座標が分かっている点）から既知点まで，新点を経由して測量していきます。
測量１回ごとに誤差が少しずつ積み重なっていくイメージです。

で，最後に既知点を観測して座標値が出るわけなんですが，もちろん，既知の座標値と差がでます。
この差を「誤差」というわけですね。

なので，観測値から「誤差」を引いてあげれば，最確値になります。
ただ，「引く」というのが分かりづらいので，【観測値に「補正量」を足すことで最確値を出す。】という考え方をします。

ここがとてもあやふやな方が多くて，調査士に限らず，測量士補でも非常に大事な考えなのですが，何か値を補正するときは，「誤差を引く」のではなく，「補正量を足す」というやり方に固定してください。

そして，補正量の算出の仕方は，「既知の値－観測値」です。これ大事。言い方を変えると「正しい値－誤った値」ってことです。「正－誤」「せいひくご」口に出してみてください。

「せいひくご」して出た「補正量」を，観測値に足すことで，最確値を求めることができます。

問題によって誤差を引いたり，補正量を足したりしている方！今後は「補正量を足す」というやり方に固定すると，変なミスが防げますよ！

（当たり前と言われそうですが，補正方法を固定していない人は本当に多いんです。そういう方は足すべきものを引いてしまったり，その逆をしてしまったり。。「誤差って足すんだっけ？引くんだっけ？」と迷っちゃうわけですね。）


■均等法のやり方

閉合でも結合でも一緒なので，ここからは閉合で説明します。
誤差の調整方法には色々あって，均等法，コンパス法，トランジット法などがあります。
でも，試験的には均等法とコンパス法を押えておけばokです。

均等法とは，「閉合を構成する各点に均等に誤差を調整する」という方法です。

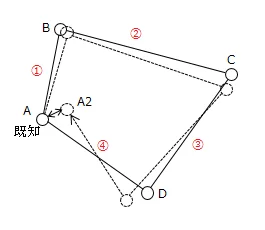
上の閉合トラバースだったら，４回観測して１周の閉合をしています。
最終的にＡ（既知点）とＡ２（観測点）には誤差が発生していますが，この誤差を観測数で割って，各点に均等に配分していきます。

例えば，補正量がX座標4mm Y座標8mmだったとしましょう。
この補正量を観測数である４で割ると，１観測数あたりの補正量がX座標1mm Y座標2mmになります。これを各点に到達するまでの観測数で配分していきます。

Ｂまでは観測数１回で到達するので，X座標1mm Y座標2mmを観測値に足します。
Ｃまでは観測数２回で到達するので，X座標2mm Y座標4mmを観測値に足します。
Ｄまでは観測数３回で到達するので，X座標3mm Y座標6mmを観測値に足します。

Ａ２にはX座標4mm Y座標8mmを足しますが，Ａの値になるので計算不要です。


■コンパス法のやり方

一方，コンパス法は観測数でなく，「各辺長で調整」していきます。コンパス法によるトラバ－ス調整は，測距と測角の精度が同程度の際に使用されますが，問題で指定された方で調整してください。

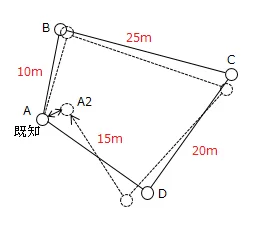
上の閉合トラバースだったら，70ｍで１周の閉合をしています。
最終的にＡ（既知点）とＡ２（観測点）には誤差が発生していますが，この誤差を辺長で割って，各点に辺長の分だけ配分していきます。

例えば，補正量がX座標7mm Y座標14mmだったとしましょう。
この補正量を総路線長である70ｍで割ると，１ｍあたりの補正量がX座標0.1mm Y座標0.2mmになります。これを各点に到達するまでの辺長で配分していきます。

Ｂまでは辺長10ｍで到達するので，X座標1mm Y座標2mmを観測値に足します。
Ｃまでは辺長35ｍで到達するので，X座標3.5mm Y座標7mmを観測値に足します。
Ｄまでは辺長55ｍで到達するので，X座標5.5mm Y座標11mmを観測値に足します。

Ａ２にはX座標7mm Y座標14mmを足しますが，Ａの値になるので計算不要です。


今回はここまで！
次回から，実際に例題を使って，複素数を使った均等法・コンパス法によるトラバース調整をやっていきましょう！！