前回，三角関数について記事にしました。
今回は三角関数を使った問題を解いてみましょう。

＜平成27　問６＞
平面直角座標系上において，点Ｐは，点Ａから方向角が230°00′00″，平面距離が1,000.00ｍの位置にある。点Ａの座標値を，Ｘ＝－100.00m，Ｙ＝－500.00m とする場合，点Ｐの座標値は幾らか。最も近いものを次の中から選べ。
なお，sin50°は「0.76604」，cos50°は「0.64279」とすること。

１ Ｘ＝－1,266.04m，Ｙ＝－742.79m
２ Ｘ＝－866.04m，Ｙ＝－1,142.79m
３ Ｘ＝－742.79m，Ｙ＝－1,266.04m
４ Ｘ＝－666.04m，Ｙ＝－142.79m
５ Ｘ＝－642.79m，Ｙ＝－766.04m

さて，いきなり「方向角が230°」と出てきます。
三角形の内角の和は180°ですから，「え！？三角形にならないじゃん！」となるわけです。
でも，こういう問題は必ず図を書いて考えましょう。
こんな感じ。

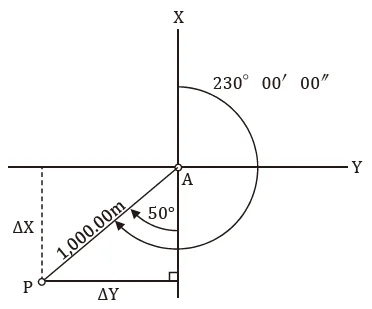
どうです？230°ですが，点Ａからの方向角（座標北からの右回りの角度のことです。）を図にすると，左下に直角三角形ができるのが分かるかと思います。
230－180＝50°を内角にもつ直角三角形です。

あとは，前回の記事を参考に，「左下に既知の内角（50°），右下に直角を置いたときの三角関数の関係」を思い出す。
すると，ΔＸは1,000×cos50°，ΔＹはは1,000×sin50°であることが分かります。
分からない方は，自分で直角三角形と筆記体で三角関数の頭文字を書いてみてください。

計算すると，
ΔＸ＝1,000×cos50°＝1,000×0.64279＝642.79ｍ
ΔＹ＝1,000×sin50°＝1,000×0.76604＝766.04ｍ
となります。

そして，もう一度，書いた図を見ます。
するとΔＸもΔＹもマイナス方向ということが分かります。つまり，ΔＸもΔＹも点Ａの座標値から引くと点Ｐの座標値となる，ということ。
本来ならば「230°は第三象限になるからcosとsinはマイナスでtanはプラスだっけ」と考えるところですが，これ，分かりづらいですよね。でも，図を書いちゃえばそんなの覚える必要ありません。

あとは，筆算なんてしなくても答えが「３」になることが分かります。
測量士補の問題は書いてある答えの中から選ぶ問題ですので，細かい計算は不要です。