測量における角度の表し方には，「180°」や「123°45′67″」などの度数法だけでなく，ラジアン（[rad]）を単位とする弧度法もあります。

測量士補の問題文の中に，「ρ」や「角度１ラジアンは，2″×10⁵とする。」という記述があれば，ラジアンを使って問題を解くことになるわけですね。

では，ラジアンとはなんでしょうか？

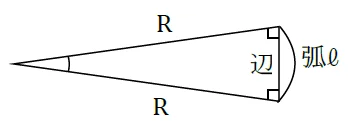
ラジアンとは，「円の半径に等しい長さの弧の中心に対する角度」のことを指します。単位は[rad]です。
分かりづらいですね。

例えば半径１の円を考えてください。

この円の中心角はもちろん，360°です。
円周の長さは半径×２（直径）×πで求めることができます。
ということは，360°は半径×２（直径）×πラジアン，つまり2π[rad]になります。

360°＝2π[rad]ですから，180°＝π[rad]となり，1°はπ÷180[rad]。
πを3.14だとすると，1°は約0.017[rad]，反対に1[rad]は約57°ということになります。この57°を秒にすると200,000″，つまり問題文にある「角度１ラジアンは，2″×10⁵（200,000″）とする。」になります。

次回は，実際にラジアンを使った計算問題をやってみましょう。