前回の記事でいきなり「正弦定理」が出てきておっと思われたかもしれません。

測量士補と土地家屋調査士試験においては，「図形」を扱いますので，三角形の定理を知っておく必要があります。

どんな図形でも補助線を引けば三角形に分解できるので，知る価値があります。
また，「定理っていっぱいあって覚えられないよ」という方。実は試験で使う三角形の定理は全部で３つです。最低３つ，ではなくて，全部で３つ。あとは使いません。

３つの定理は，「ピタゴラスの定理」，「正弦定理」，「第２余弦定理」。この３つだけです。
１つずつ見ていきましょう。

①　ピタゴラスの定理
ピタゴラスの定理は，「直角三角形において，短辺の２乗の合計が長辺の２乗に等しくなる。」という定理です。

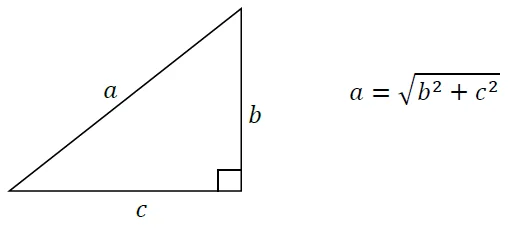
直角三角形のみに使える定理だということに注意してください。でも，どんな三角形だって，補助線を引けば直角三角形に分割できますから，非常に幅広く使える便利な定理です。
色々なところで使います。

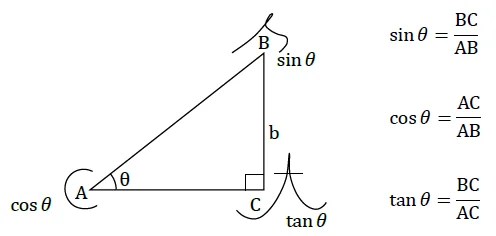
②　正弦定理
正弦定理は，「ある内角のsinと，向かい合う辺の比率はどれも等しくなる。」という定理です。

これはピタゴラスの定理と違って，直角三角形に限りません。あらゆる三角形に使えます。
前回やった偏心補正計算では，この正弦定理と微小角計算を組み合わせて問題を解くことになります。
使うのは測量士補試験の偏心補正計算だけですが，土地家屋調査士試験でも使えることがあります。でも，使えるだけで，使わないと解けない問題は出題されません。電卓で座標計算ができますから。

③　第２余弦定理
第２余弦定理は，「三角形の辺長が分かっている場合，その内角が求まる。」という定理です。

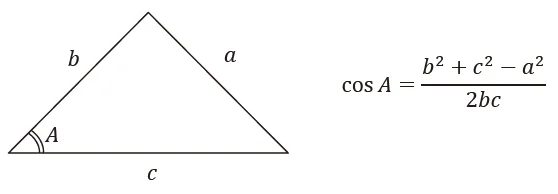
これもあらゆる三角形に使えます。
測量士補試験では使いません。
「え？距離の偏心補正って第２余弦定理を使うんじゃないの？」という方。よく勉強しています。
でも，第２余弦定理を使わなくても，微小角計算で答えを出すことができます。これは別の機会に。
つまり，測量士補試験で言えば，覚える定理はピタゴラスの定理と正弦定理の２つだけですね。

じゃ第２余弦定理っていつ使うのかというと，土地家屋調査士試験です。
逆計算で使います。逆計算というのは，２点の座標値が与えられ，その２点からの点間距離だけが判明している新点の座標値を求める場合。でも，絶対に知らないと解けない問題は出題されていません。他のアプローチが用意されています。例えば，おしかったのが平成25年問21のE点ですね。第２余弦定理を使「っても」座標値を求めることができます。
ただ，今後第２余弦定理を使「わないと」座標値が求められない問題が出るかもしれませんので，押さえておきましょう。