複素数ミニ講義の15回目です。

いよいよ最後のテーマであります，求積をやりましょう。土地の地積を求める計算ですね。

いままでの電子書籍などではオーソドックスな方法しか紹介していませんでしたので，このミニ講義では四角形の土地に限定した簡易な方法もご紹介します。

今回は実戦前の大事なこと編をお送りいたします。準備編でも理論編でもなく，求積する上での「大事なこと」をお伝えします。

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

■求積

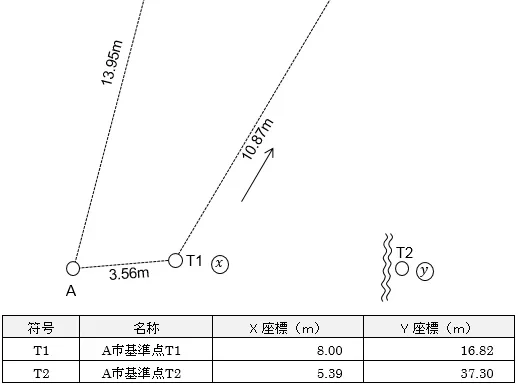
調査士試験問21の土地では，必ず求積の計算をすることになります。

地積測量図に求積表と地積を記載することもありますが，近年は記載省略の方向です。
ですが，地積を計算しないと，「地積更正登記がいるのか？」という超重要判断ができません。また，土地の地積だけを解答するような問題もあります。

よって，必ず求積の計算をすることになると言ってよいでしょう。

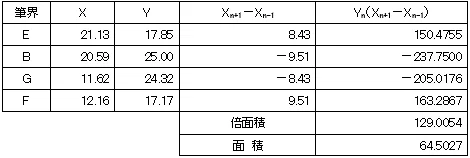
地積測量図に求積表の記載が求められることもありますので，下のような求積表を書けるようにしておいた方がよいです。

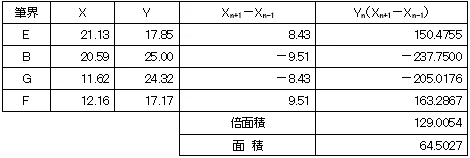
と言っても，求積表の書き方や理論は測量士補の応用測量のとこで学習するんですけどね。
まぁ，前にも言いましたが，近年は求積表の記載を省略する問題が多いですが。

■四捨五入のタイミング
 

ただし！じつはこの求積表にはめちゃくちゃ大事な要素があります。コレを伝えるための記事でもあります。
それは，座標法による求積というのは，求積表を見てもらえば分かるように，小数点以下第３位を四捨五入した座標値で計算するんですね！
なので，複素数を使って求積する場合も，四捨五入した座標値で計算する必要があります。

よく，「複素数だと答えの数値が通常の計算と違う」と思っている方が本当に多いんですが，これは誤解です。アプローチの仕方は異なりますが，通常の計算も複素数の計算も中身は一緒！一緒なんですよ！なので，「複素数だと答えの数値が通常の計算と違う」という理由はほとんどが「四捨五入のタイミング」を誤っているからです。

（現在販売中のkindleの電子書籍でもこの辺りが固まっていなかったので，７月のアップデートで無料更新いたします。申し訳ありません。）

で，「じゃいつ四捨五入するんだ？」と言うと，①辺長の計算 ②求積，いずれかの直前です。
この辺りは，kindle電子書籍やアガルートの複素数講座で取扱っている練習問題の中で，全体の流れを踏まえて解説しています。よろしければ。

この点を誤らなければ，複素数でも通常の計算でも答えはぴったり一緒になりますよ。

それでは，次回から，求積の実践をやっていきましょう！！！