複素数ミニ講義の14回目です。

本日はkindle書籍（中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】）に書いていない内容です！
このミニ講義を踏まえて無料にてアップデート予定です。

その内容とは・・・「逆計算」です。
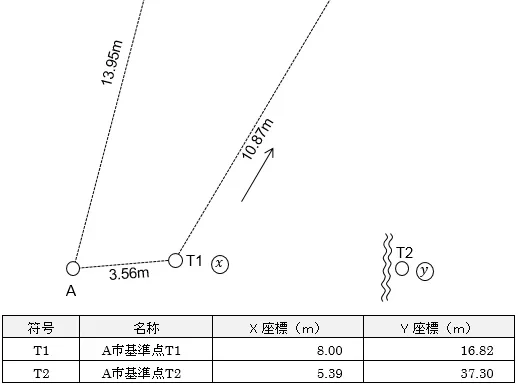
逆計算とは，２点の座標値が与えられ，その２点からの点間距離だけが判明している新点の座標値を求める計算方法になります。

点間距離しか分かってないので通常の交点計算が使えないんですね。

ちなみに，調査士本試験では「逆計算を使えないと解けない問題」というのは出題されていません。問題公表前の本試験問題は今の出題形式とかけ離れているので無視。
「逆計算を使っても解けるけど，他の方法でも解ける」ってな感じですね。

でも，これから先，逆計算ができないと座標値が出ない問題が出題されないとも限らないため，しっかりと練習しておきましょう。

★★★★★★★★★★★★★★★★★★★★★

テキストを使って実際に電卓操作を見ながら学べるアガルートの講座はコチラ↓

アガルート【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】

▼　サンプル講義の動画もどうぞ！

amazon kindleの電子書籍はコチラ↓

中山祐介【複素数で解く！関数電卓による測量計算: 土地家屋調査士試験、測量の実務現場で早い！使える！ Kindle版】

★★★★★★★★★★★★★★★★★★★★★
 

■逆計算

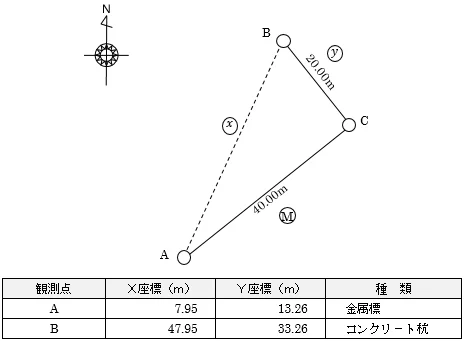
それでは実際に，A点から北東側に40.00ｍ，B点から南東側に20.00ｍに位置するC点の座標値を求めます。
ちなみに，この逆計算。けっこう他の複素数計算と違う面が多々ありますので，慣れが必要です。
まず，大きな違いが「定理を使う」ということ。測量士補を学習された方なら理解されていると思いますが，「第２余弦定理」を使います。

第２余弦定理とは，こんな定理です↓

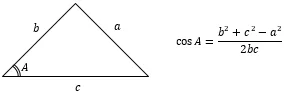
直角三角形に限らず全ての三角形に使える非常に便利な定理です。平成30年度の測量士補試験でも第２余弦定理を使う問題が問３で出題されたので，調査士・測量士補を受験する方はしっかりと覚えておいてください。
３つの辺長が既知のときに，１つの角（上の図なら∠A）を計算で求めることができます。

では，問題をやってみましょう。繰り返しますが，C点の座標値を求めます。

■座標の入力

まずは，既知のA点とB点をそれぞれメモリ「A」と「B」に記憶させます。

①A点をAに記憶させる

②B点をBに記憶させる

■辺長の入力

第２余弦定理では既知の３つの辺長を使います。
ところが，問題には２辺（BCとAC）しか出ていないですね。そこで，辺ABの距離を点間距離の計算によって求めます。
辺ABはメモリ「x」に，問題文にあるBCとACの各辺長は，それぞれ「y」と「M」に記憶させることにします。

③AとBの点間距離を求め，xに記憶させる

④辺長BCをyに記憶させる

⑤辺長ACをMに記憶させる

これで全部の記憶が済みました！
ちなみに，記憶させたメモリ名で余弦定理を改めて書くと，このようになります。

■第２余弦定理

では，関数電卓の操作で，この余弦定理を解いていきましょう。
最終的にはcosθの値が算出されますので，cosを取ってあげる必要があります。cosθの値をθにするためには，逆三角関数「cos^-1」（アークコサイン）を使います。
「cos^-1」は[SHIFT] [cos]で使うことができますよ！

では，このθを計算してメモリ「C」に記憶させるとこまで一気にやってみましょう。
定理の式を良く見ながら，電卓操作をしてみるのがいいです。

⑥３辺の長さが既知の三角形の内角θを求めて，Cに記憶させる

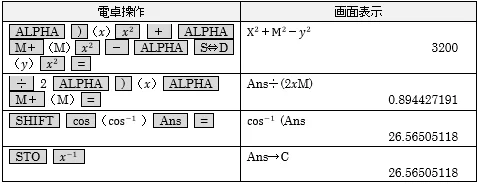
どうですか？できましたか？
このθというのは∠BACになります。なので，AからBの方向角にθを加えて40.00ｍ移動した点を求めると，C点の座標値がでるわけですね。通常の放射計算と同じです。

⑦AからBの方向角を求める

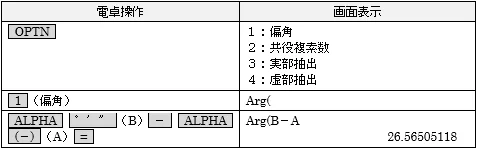
⑧方向角と距離で座標を出す

これでC点の座標値は「X座標31.95ｍ，Y座標45.26ｍ」と求めることができました！

いかがでしたでしょうか？？
定理を使うんですが，複素数だから間の計算（点間距離を出したり，放射計算をしたり…）を早くすることができました。

ちなみに，逆計算で座標を計算した場合，他の座標との点間距離を計算して，座標値が確かであるか確認すると良いでしょう。簡単に点検することができます。

アガルートの【土地家屋調査士試験 | 2018合格目標 複素数で解く測量計算】では，この逆計算も含め，kindleにはまだ載っていない計算方法も紹介しています。また，テキストも電子書籍ではなく，通常のテキストのような印刷されたものになります。講義は動画形式なんですが，私が実際に電卓操作しているところが見れるので，非常に分かりやすいですよ！


それでは！本日は逆計算でした！
次回は面積計算をやります。