前回，ラジアンについての記事を書きました。
今回はラジアンを使った計算問題を解説します。

ラジアンを使うのは「微小角」の問題です。
微小角とは，とっても小さい角度のこと。微小角の問題はラジアンを使うと便利なんですよ。

例えば，下の図を見てください。

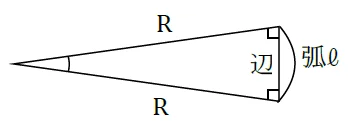
二等辺三角形ですが，左の内角が微小角です。とっても小さい角度なので，他の２つの内角を直角とみなすことができます。
三角形の内角の合計は180度なので，本来直角が２つあるというのはあり得ないのですが，微小角が小さいため，このようにみなすことができてしまいます。

ラジアンを計算するには，孤の長さを半径で割って求めます。で，これが微小角ですと，直角が２つあるので，孤をほぼ直線とみなすことができます。つまり，対辺÷斜辺，あるいは対辺÷底辺。

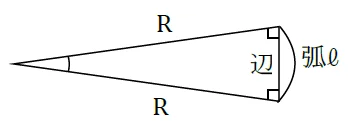
下の図を見てください。

実はこの「みなし」を使うと，面白いことになります。
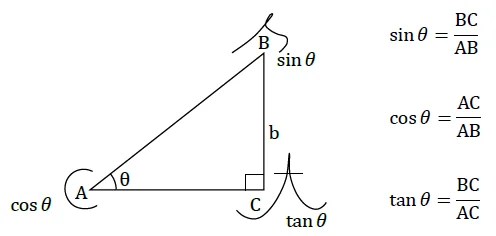
三角関数で，sinは対辺÷斜辺，tanは対辺÷底辺です。これ，ラジアンと同じです。
つまり，微小角においてラジアン＝sin＝tanということになります！

測量士補の計算問題だと，角度の偏心補正計算（距離の偏心補正計算でも使えますが，それはまたの機会に）。

こんな問題ですね。
θの角度を求めるとほぼ答えが出るんですが，このθ，正弦定理を使ってもsinθの値しか求まりません。
ですが，θは微小角なため，sinθをθ[rad]とみなすことができるんです。
例えば，正弦定理を使って，sinθが0.0045と求まりました。
θ[rad]とみなすことができるため，前回の記事で紹介したρ（2″×10⁵）をかけることで，度数法に変換できるわけです。

0.0045×2″×10⁵＝450×2″＝900″＝15′

↑となります。

sinθの値だけでθの角度を求めることができる，というお話でした。