さて，土地家屋調査士の令和３年度本試験において，中山がずっと言っていた「申請人欄の難化」でいくとこまでいってしまったので，次来るとしたら（「計算の手数の多さ」は引き続き予想されるところですが），計算アプローチの難化でしょう。

問21土地を解いていて，座標が計算できなかった時の焦りといったら想像するだけで冷や冷やします。
そんな中，計算アプローチとして，多くの方から苦手とご報告いただくのが，「面積指定の分割」です。売買契約や遺産分割によって，地積が指定されており，その指定された地積になるよう，分割点を新設することなどが問題として想定されます。

そのような場合，まず考えていただきたいのが，「すべての土地は三角形に分割することができる」という点です。
どのような多角形の土地であっても，三斜求積図のように三角形に分割することができます。
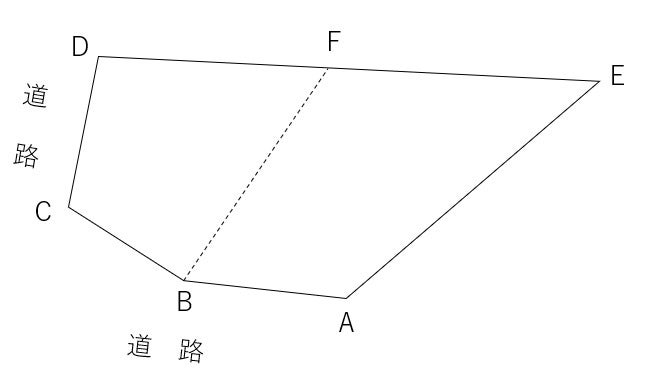
そして，面積指定を考えなければならない図形を，１つの三角形にするところまで追い込みます。例えば，以下のいびつな土地。

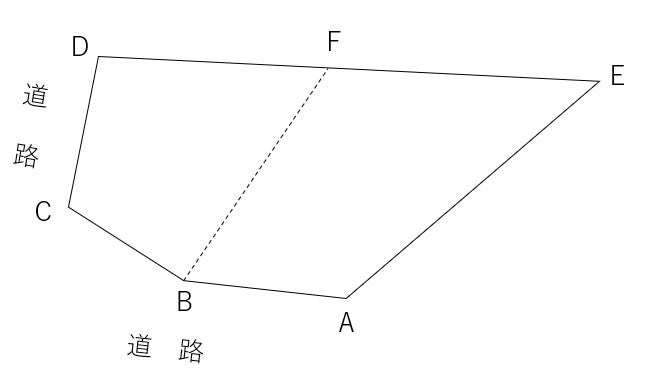
これを，B点を分割点の１つとして，直線DE上にF点を分割点として新設したい。との問題が出たとします。
座標値は，以下のとおりです。

点名　X座標　Y座標
A　100.00　100.00
B　101.10　 91.20
C　106.50　 85.30
D　113.40　 86.70
E　111.40　113.80

分割後の西の土地を100平方メートルにすることにしましょう。

まず，△BCDは，既知点の集合なので，座標を出すことができます。

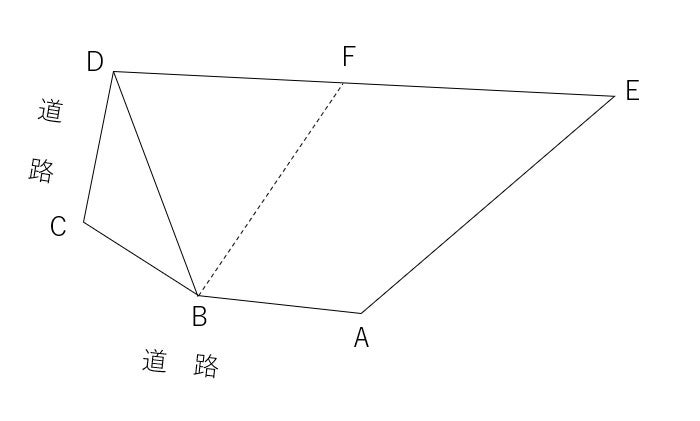
計算すると，24.135㎡になります。ということは，△BDFが，100－24.135＝75.865㎡になればよいことになります。
こうして，面積指定を考えなければならない図形を，１つの三角形にするところまで追い込むのが最初にやることです。

つぎに，三角形の面積について，少し考えてみましょう。
三角形の面積は，どのように計算しますか？

もちろん，「底辺×高さ÷２」ですね。

上の三角形ですと，面積（S）＝1/2AC・ hとなります。20×20÷2＝200平方メートルですね。面積が指定された三角形の底辺か高さのどちらかが分かっていれば，もう一方を計算で出すことできます。
先ほどの問題でいえば，既知点であるBDを底辺にして考えてあげることで△BDFの高さが分かりますから，交点計算等でF点を計算することができます。具体的には，高さが，76.865×2÷Abs（B－D）で求まるので，交点計算によりF点をもとめることができます。計算すると，F点は，X座標112.46ｍ，Y座標99.38ｍになりますね。

ちょっとご質問があったので，F点の計算について加筆します。
△BCDの面積は，
　Conjg（B）C＋Conjg（C）D＋Conjg（D）B＝
　Ans÷2＝
　ImP（Ans＝
で，24.135とでるので，△BDFの面積は，
　100－Ans＝
で，75.865です。
BDを底辺とした場合の△BDFの高さは，
　Ans×2÷Abs（B－D→M
で，11.5848…となります。Mにストアしときました。
この高さは，DからBの方向角に－90度した方向の長さになりますので，計算点として，M点を作ります。
　Arg（B－D＝
　D＋M∠（Ans－90→M
これで，F点は，M点から出る「DからBの方向角」の直線と，直線DEの交点になります。
あとは，交点計算です。
　Arg（B－D→x
　Arg（E－D→y
　tan（x）＋i→x
　tan（y）＋i→y
　Mx－Dy＝
　Ans÷（x－y＝
　ReP（Ans→F
　Ans－M＝
　Ans× x＝
　ReP（Ans＝
　F＋Ans×i→F
これで，F点の座標値が（四捨五入すると）X座標112.46ｍ，Y座標99.38ｍとなり，Fにストアされました。
追記は以上です！

では，他に，三角形の面積を求める方法はどのようなものがあるでしょうか？これが本題です。
まず，２辺の長さとその夾角が決まっているパターンです。

この場合，高さ（h）は，AB・sin（30°）＝20ｍと求めることができます。ですので，20×20÷2＝200平方メートルですね。２辺が分かっていれば夾角が，夾角と１辺が分かっていればもう一方を計算で出すことが出来ます。

式にすると面積（S）＝1/2AC・AB・sinθとなります。

次は，３辺の長さが決まっているパターンです。

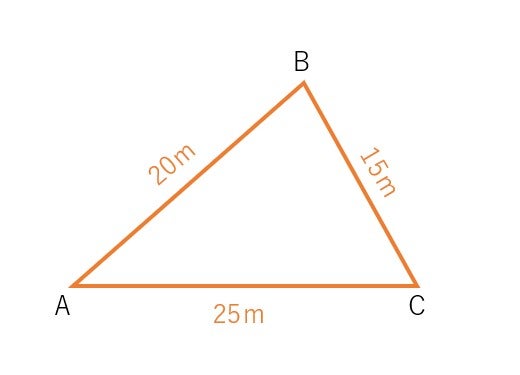
ここで使うのは余弦定理です。余弦定理は，測量士補を学習した方なら馴染みがありますね。調査士だと，逆計算で触れています。
余弦定理では，例えば，∠CABをθとすると，

　BC²＝AB²＋AC²－2・AB・AC・cosθ

になるため，θを求めることができます。

計算すると，
15²＝20²＋25²－2・20・25・cosθ
225＝400＋625－1000・cosθ
cosθ＝800÷1000
cosθ＝0.8

あとは，アークcos（0.8）をやることで，∠CABを求めることができます。
そうすると，２辺の長さとその夾角が決まっているパターンと同じになりますので，高さ（h）は，AB・sinθ＝12ｍと求めることができます。この三角形の面積は，25×12÷2＝150平方メートルですね。逆計算と同じですが，２辺が求まっていれば，残りの１辺の長さ（または，２辺の夾角）を計算で出すことが出来ます。
面積だけなら，ヘロンの公式でも行けます。

いかがでしょうか？

これらを応用することで，どのような土地の面積指定でも計算することができます！

変な問題ですが，「底辺×高さ÷２」が三角形の面積という基本さえ分かっていれば，下の△ECDの面積も一瞬で分かります。

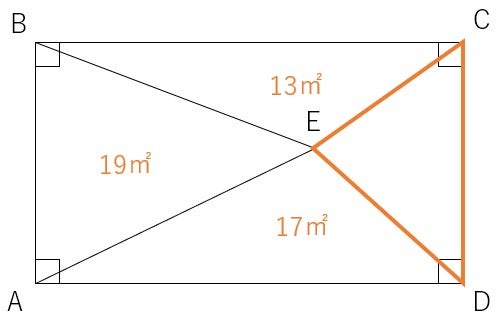
それでは！