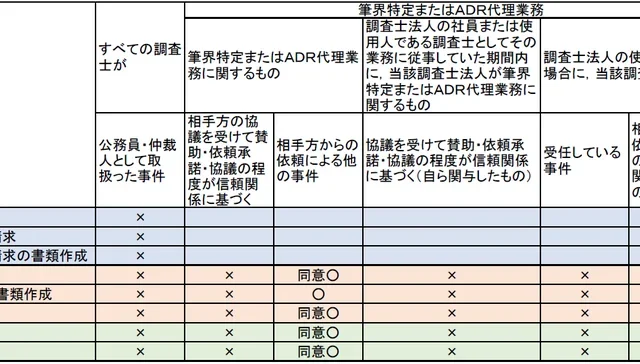
方向角90°の交点計算について
本ページにはプロモーションが
含まれていることがあります
ひとえに「複素数」といっても,複素数を使った計算方法には色々な方法があるわけです。
もちろん,全部検証して,使えるものは導入したり修正したりしているワケですが,その中でも「使いやすいもの」を取捨選択して,[中山式]複素数計算として採用しています。
「使いやすいもの」というのも曖昧ですが,計算方法が直感的でないものや,例外が多いものは積極的に省いています。
で,今回話題にしたいのは,「方向角90°」の交点計算です。
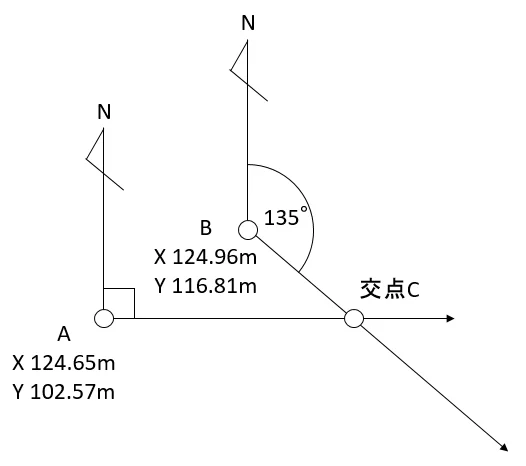
下図のようなものです。
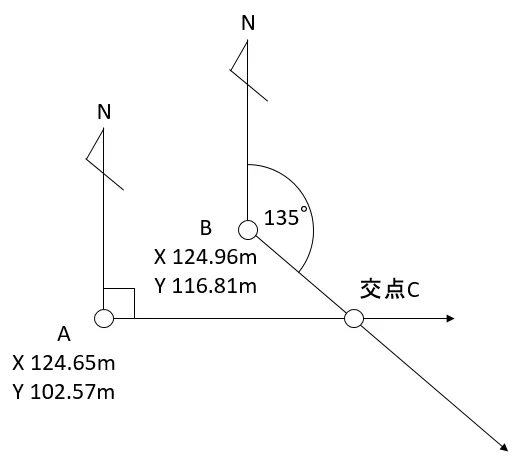
点A(X 124.65 Y 102.57)から方向角90°,点B(X 124.96 Y 116.81)から方向角135°にある交点Cを求めてみます。
交点計算では,2つの方向角を「tan(x)+i→x」,「tan(y)+i→y」にそれぞれ加工してから使用しますが,これが問題です。というのも,tan(90°)は数学的にあり得ないので,解なしになってしまうんですね。
なので,今までは「90°0′0.0001″」を入れてやろう!と言っていたんですが,これだと解けない例外が出てくるし,答えが合わない場合が出てくるしで良いことがありません。特に大きいのが,【使用する電卓や設定によって計算結果に差異がある】という点です。
よって,今後は,このやり方はなし!やってはいけない方法にします。
では,どのようにするかと言えば,方向角90°ではない方向角のみを使用します。
というのも,交点CのX座標は,方向角が90°であるため,点AのX座標と同一になります。つまり,X座標はもう計算する必要はなし。
なので,点Bからの方向角135°のみを使用します。具体的にはこんな感じ。
124.96+116.81i→B
tan(135)+i→Y
(124.65-B)✕Y=117.12+116.5i
↑この実数部(117.12)が,交点CのY座標になるので,答えは(X 124.65 Y 117.12)となります。
通常の交点計算のX座標を求めるところまでを一気に飛ばし,Y座標のみ計算する方法です。
ただ飛ばすだけなので,新しいことを覚える必要はないし,結果的に早く計算できます。是非,こちらの方法に改めてください。
それでは!