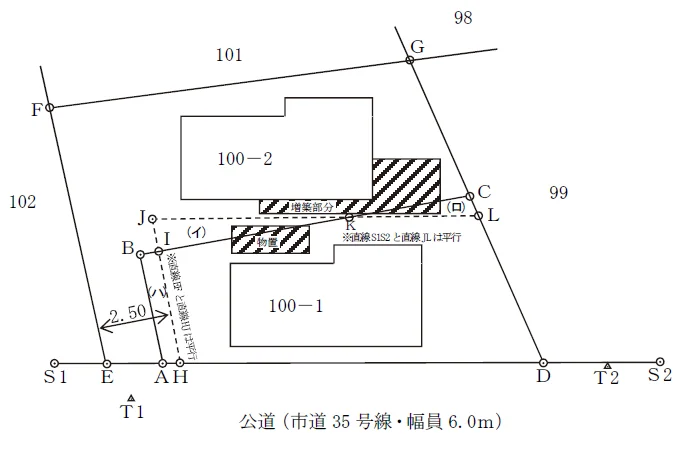
土地家屋調査士試験の平成21年度本試験問21土地。
台形の図形的特徴を踏まえて二次方程式を使って解くことになるので，苦手な方が多い問題です。

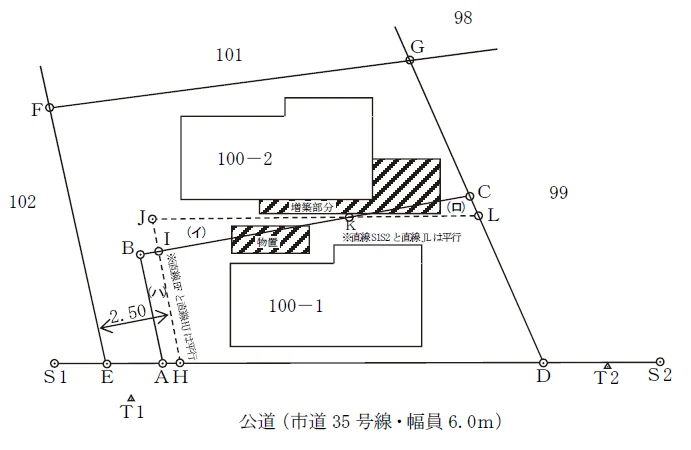
二次方程式については，関数電卓の「方程式計算モード」がありますので，これを使った解法を解説することが多いですが，今回は，ちょっと違うアプローチで解いてみましょう。
直角三角形の図形的特徴を使う方法です。

まずは，お手元に平成21年度問21をご用意下さい。（この記事を読む前に，改めて一度解いておいてもらうと分かりいいと思います。）
Ｈ点とＩ点をそれぞれ交点計算で求めるところまでは一緒です。Ｊ点を違うアプローチで出してみましょう。

まずは，直線ＨＪと直線ＤＬの交点をＭ点として補助点を出します。これは通常の交点計算です。「Ｅ点からＦ点までの方向角（0°）でＨ点から出した直線」と，「Ｄ点からＣ点の方向角でＤ点から出した直線」の交点計算等で計算することができます。
計算すると，Ｍ点の座標値は，（550.27，485.26）となります。
図にするとこんな感じです。

上の図の大きな三角形△HMDの面積は，「底辺×高さ÷2」で求められますので，12.5×50÷2＝312.5㎡となります。
（底辺は，Ｄ点ｙ座標497.76－Ｈ点ｙ座標485.26＝12.5ｍ。高さは，Ｍ点ｘ座標550.27－Ｈ点ｘ座標500.27＝50.0ｍですね。）

一方，上の図の台形□HJLDの面積は，問題中の「分筆前の乙土地」の面積と同じになりますので，B，C，D，A及びBを座標法（Conjg使うやつ）で求積して，100.3367㎡と求めることができます。

ということは，上の図の小さな三角形△JMLの面積は，312.5－100.3367＝212.1633㎡となります。
図にするとこんな感じになります。

「大きな三角形△HMD」と，「小さな三角形△JML」は相似の関係にあります。
相似の三角形なので，高さが2倍になっていれば，底辺も2倍になっているので，面積は4倍（2²）。高さが3倍になっていれば，底辺も3倍になっているので，面積は9倍（3²）。
つまり，高さがｎ倍になれば，底辺もｎ倍になり，面積はｎ²倍になります。
逆に，面積がｍ倍になっていれば，高さと底辺は√ｍ倍になります。

では，「大きな三角形△HMD」の面積は，「小さな三角形△JML」の面積の何倍でしょうか？
計算すると，312.5÷212.1633＝1.472922037倍です。
ということは，「大きな三角形△HMD」の高さ（HM点間距離）は，「小さな三角形△JML」の高さ（JM点間距離）の√1.472922037＝1.213639995倍になることが分かります。

「大きな三角形△HMD」の高さ（HM点間距離）は，Ｍ点ｘ座標550.27－Ｈ点ｘ座標500.27＝50.0ｍですので，「小さな三角形△JML」の高さ（JM点間距離）は，50÷1.213639995＝41.19837861ｍとなります。
よって，Ｊ点のｘ座標は，Ｍ点から41.19837861ｍ方向角180°に移動した，550.27－41.19837861≒509.07ｍとなります。ちなみにＪ点のｙ座標は，Ｍ点やＨ点と同じ485.26ｍ。

Ｌ点のｘ座標もＪ点のｘ座標と同じ509.07ｍですし，ｙ座標は交点計算で求めてあげればokです！

それでは！