今回は，応用的な問題として，セットバックを複素数でやってみましょう。

セットバックは，交点計算の一種ですが，仮点をつくったり，方向角を理解していなければならなかったりと，論点が多く，苦手な方もいらっしゃいます。

みてみましょう。

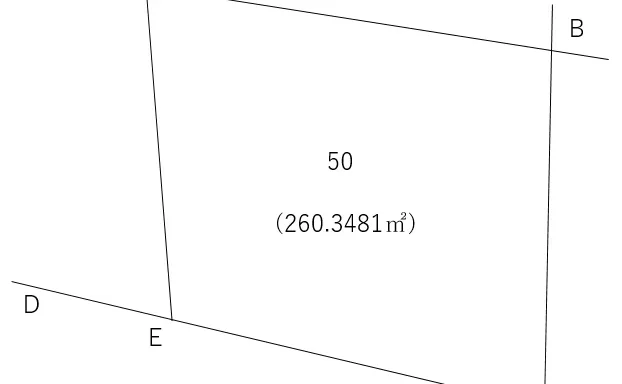
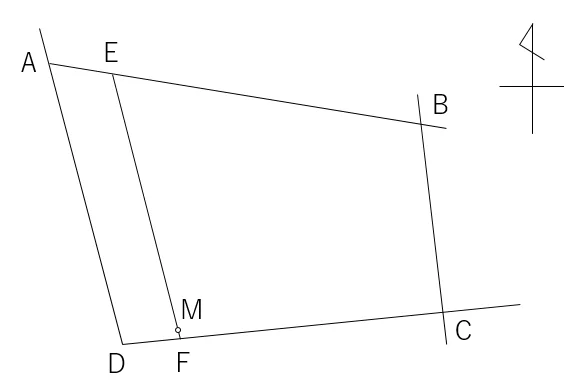
例えば，↓の図のような，四角形ＡＢＣＤの土地があります。

＜座標＞
Ａ　Ｘ座標：118.00ｍ　Ｙ座標： 97.00ｍ
Ｂ　Ｘ座標：115.00ｍ　Ｙ座標：115.00ｍ
Ｃ　Ｘ座標：101.00ｍ　Ｙ座標：118.00ｍ
Ｄ　Ｘ座標：100.00ｍ　Ｙ座標：100.00ｍ

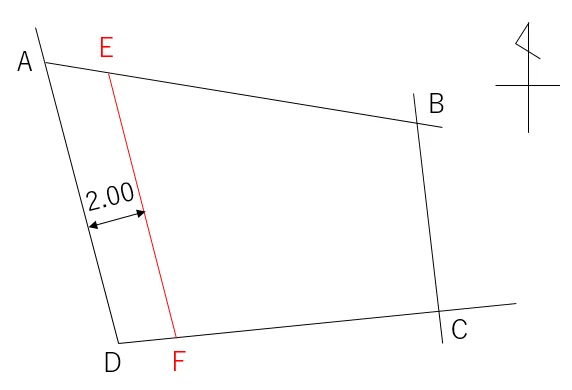
このＡＢと平行に2.00ｍ東側にセットバックしてみます。セットバック点はＥ点・Ｆ点とします。
まずは，ＡＢＣＤの各点を，それぞれメモリＡＢＣＤにストアしておきます。

118＋97ｉ→Ａ
115＋115ｉ→Ｂ
101＋118ｉ→Ｃ
100＋100ｉ→Ｄ

セットバックは交点計算なのですが，直線ＦＥ上の点がありません。
なので，まずは直線ＦＥ上に，仮点（計算点）として「Ｍ点」をつくります。
Ｍ点の候補しては，下の図のように２つあります。

Ｍ①はＡから2.00ｍ，Ｍ②はＤから2.00ｍの距離です。

「ＡからＭ①の方向角」と「ＤからＭ②の方向角」は同じになります。この方向角は，直線ＡＤと直角に交わる方向です。
この方向角の求め方も２つあります。

ＡからＤの方向角から「－90°（＋270°）」する。
ＤからＡの方向角から「＋90°」する。

どちらでもよいです。方向角は「右回り」の角度ですので，プラスなのかマイナスなのかは，「ＡからＤの方向角」と「ＤからＡの方向角」のどちらを使うかによって使い分けます。よく図をみて間違えないようにしてください。

Ｍ①とＭ②はどちらかを採用すればよいので，今回はＭ②にしましょう。
Ｄ点からの距離は2.00ｍ，Ｄ点からの方向角は「ＤからＡの方向角＋90°」です。点の移動です。
ＤからＡの方向角を求めた後，点の移動をしています。求めたＭ②点はメモリＭにストアします。

Arg（Ａ－Ｄ＝
Ｄ＋2∠（Ans＋90→Ｍ（100.328…＋101.972…ｉ）

次はＥとＦを交点計算で求めます。
まずはＥを求めましょう。交点計算をするための図はこんな感じ。

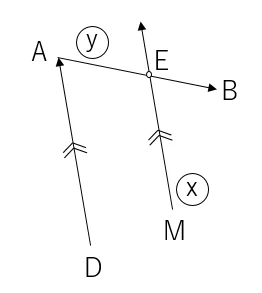
ＭからＥの方向角を「ｘ」，ＡからＢの方向角を「ｙ」とします。
で，この方向角ｘですが，平行移動なので，「ＤからＡの方向角」と同じになります。
なので，方向角ｘは，ＤからＡの方向角を求めることになります。

Arg（Ａ－Ｄ→ｘ
Arg（Ｂ－Ａ→ｙ

あとは，通常の交点計算です。メモを使わずに，途中でＥのＸ座標をＥにストアしてます。

tan（ｘ）＋ｉ→ｘ
tan（ｙ）＋ｉ→ｙ
Ｍｘ－Ａｙ＝
Ans÷（ｘ－ｙ＝
ReP（Ans→Ｅ
Ans－Ｍ＝
Anx×ｘ＝
ReP（Ans）ｉ＋Ｅ→Ｅ（117.652…＋99.085…ｉ）

これで，Ｅの座標値がＸ座標：117.65ｍ　Ｙ座標：99.09ｍと計算できました。
続いて，Ｆも計算しましょう。交点計算をするための図はこんな感じ。

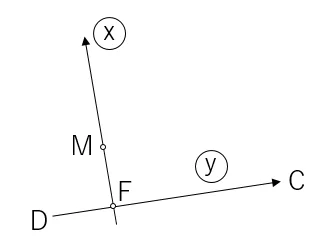
方向角ｘは，前のＥを求めるところで加工（tan（ｘ）＋ｉ）までしているので，そのまま使います。
「ＭからＦの方向角は，方向角ｘと正反対なんじゃない？」と思われたかもしれませんが，関係ありません。実は交点計算の方向角は180°反対向きでも正確に計算することができます。

なので，求めるべきはＤからＣの方向角ｙだけです。
やってみましょう。メモを使わずに，途中でＦのＸ座標をＦにストアしてます。

Arg（Ｃ－Ｄ→ｙ
tan（ｙ）＋ｉ→ｙ
Ｍｘ－Ｄｙ＝
Ans÷（ｘ－ｙ＝
ReP（Ans→Ｆ
Ans－Ｍ＝
Anx×ｘ＝
ReP（Ans）ｉ＋Ｆ→Ｆ（100.111…＋102.008…ｉ）

これで，Ｆの座標値がＸ座標：100.11ｍ　Ｙ座標：102.01ｍと計算できました。


それでは！