問１＜機器の点検（三点法）＞

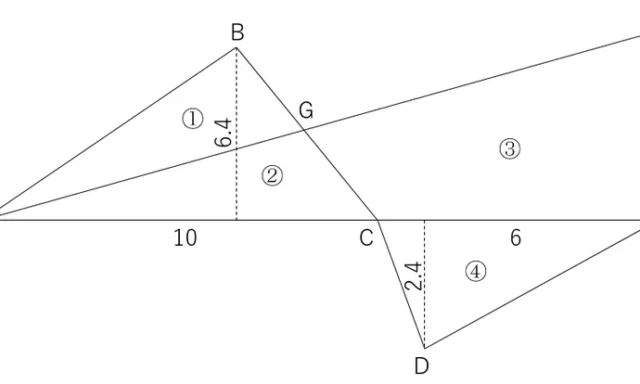
三点法による測定距離の補正を計算する問題である。

距離の補正値（器械定数と反射鏡定数の和）は，AC－（AB＋BC）で求まる。

①器械定数と反射鏡定数の和を求める
595.55－(297.51＋298.06＝

②AC間の補正後の距離を求める
595.55＋Ans＝

以上により，AC間の補正後の距離は595.53と求められた。
よって，正解は「２」である。

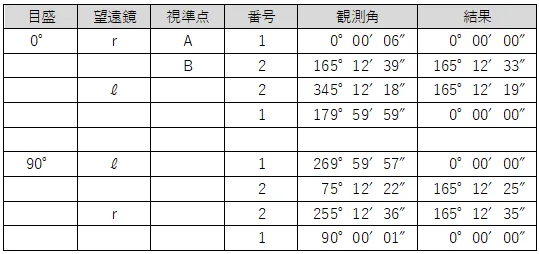
問２＜観測手簿（水平角）と標準偏差＞

観測値から，水平角の最確値と標準偏差を計算する問題である。

まずは，「結果」を計算する。
結果は，新点（Ｂ）の観測角から基準となる点（Ａ）の観測角を引くことで計算する。

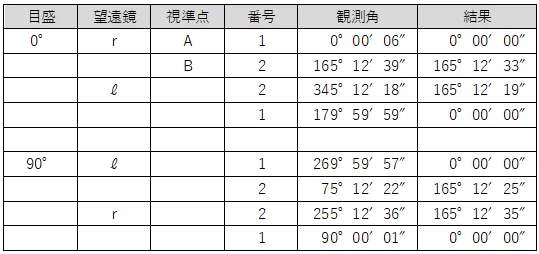
Ｂの結果は，165°12′33″，165°12′19″，165°12′25″，165°12′35″であるため，これを平均することで最確値を求める。

まずは，それぞれの観測値をメモリ「Ａ」から「Ｄ」までに記憶させる。
計算を簡略化するため，165°12′を基準とした。

①結果をＡからＤに記憶させる
33→Ａ
19→Ｂ
25→Ｃ
35→Ｄ

結果の平均値（最確値）を求める。

①結果の平均値を求めてｘに記憶させる
Ａ＋Ｂ＋Ｃ＋Ｄ＝
Ans÷4→ｘ

ｘは28″となるため，ＡからＢの水平角は，165°12′28″と求められた。

次に，最確値の標準偏差を計算する。
最確値の標準偏差（M）は以下の式で求められる。n＝観測回数，v＝残差とする。残差とは，平均値（最確値）と各観測値の差をいう。

各観測値の残差（v）を求める。
それぞれメモリ「Ａ」から「Ｄ」までに上書きする。

②観測値の残差を求める
Ａ－ｘ→Ａ
Ｂ－ｘ→Ｂ
Ｃ－ｘ→Ｃ
Ｄ－ｘ→Ｄ

各結果の残差を二乗して合計する。

②の残差を二乗して合計してｘに記憶させる
Ａ²＋Ｂ²＋Ｃ²＋Ｄ²＝

最確値の標準偏差を求める。

①最確値の標準偏差を求める
√(Ans÷(4×(4－1＝

以上により，最確値の標準偏差は3.6968…と求められた。
よって，正解は「３」である。

問３＜GNSS測量における注意点＞

ア　×
トータルステーションによる多角測量と異なり，点から点を直接視準する必要がないため，観測点間の視通がなくても点間距離と方向を求めることができる。

イ　〇
衛星からの電波を受信するのはGNSS測量機のアンテナ部分であるため，アンテナから測点までの高さはミリメートル単位で計測しておく必要がある。高さは向きと異なり，各点で統一する必要はない。

ウ　×
衛星からアンテナまでの距離の誤差が観測位置に与える影響を少なくするため，衛星は上空に可能な限り広がり，片寄らない配置であることが望ましい。

エ　〇
GNSS測量機は衛星からの電波を受信する必要があるため，上空視界を妨げるような障害物のある場所では観測をすることができない。

オ　×
GNSS測量機は観測に光波を用いないため，霧や弱い雨にほとんど影響されずに観測をおこなうことができる。

よって，正しいものはイ，エであり，その組合せは「４」である。

問４＜点の移動と内分点＞

まずは，Ｐ点の座標値を点の移動により求める。
Ｐ点は，問題文から，Ａ点から方向角117°154′3″に8.00ｍ移動した点である。
Ａ点とＣ点を，それぞれＡとＣに記憶させる。
253.4＋300.3ｉ→Ａ
231.5＋259.6ｉ→Ｃ

点の移動により，Ｐ点を求める。Ｐ点は，Ｄに記憶させる。
Ａ＋8∠117°154°3°→Ｄ

以上により，Ｐ点の座標値は，Ｘ座標249.656…，Ｙ座標307.370…と求められた。

次に，内分点によりＱ点の座標値を求める。
Ｑ点は，問題文から，Ｃ点とＰ点（Ｄ）を2:1に内分する点である。

Ｄ－Ｃ＝
Ans÷3×2＋Ｃ＝

以上により，Ｑ点の座標値は，Ｘ座標243.604…，Ｙ座標291.446…と求められた。

よって，正しいものは「５」である。

問５＜間接水準測量＞

間接水準測量によって新点の標高を計算する問題である。
既知点（高さが分かっている点）に器械を整置し，新点（高さを知りたい点）を観測する「正方向」の間接水準測量であるため，両差（ｋ）を足すことに注意する。

正方向による間接水準測量では，以下の式で新点Ｂの標高（HB）を求めることができる。

　HB＝HA＋iA－sinα×D－fB＋ｋ

代入すると，以下のようになる。

　HB＝150＋1.5－(sin(3°43°35°)×1220)－1.45＋0.1

以上により，新点Ｂの標高（HB）は70.859…と求められた。
よって，正解は「５」である。

▲まとめ に戻る！▲