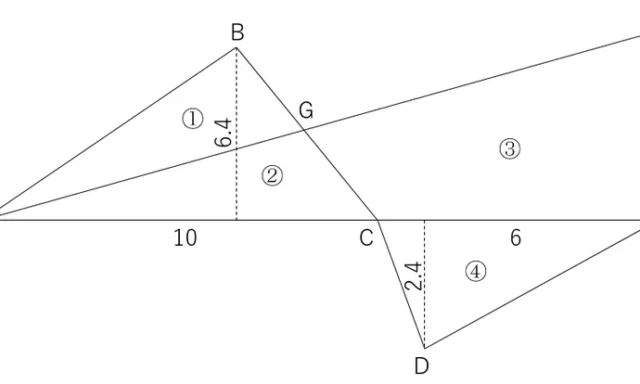
調査士<午前の部>解説ミニ講座 平成30年度 問1~5
本ページにはプロモーションが
含まれていることがあります
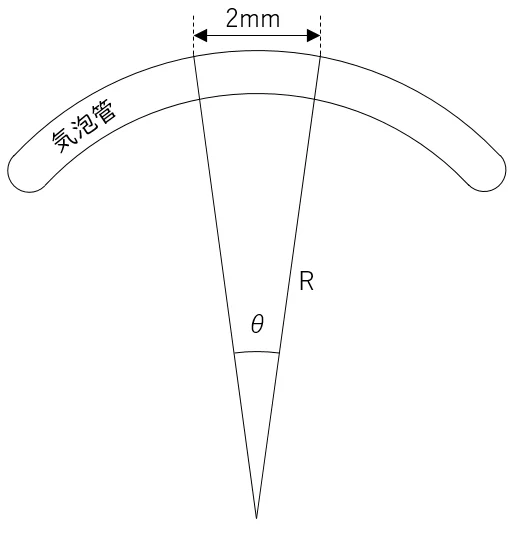
問1<気泡管感度>
管形気泡管の曲率半径を求める計算問題である。
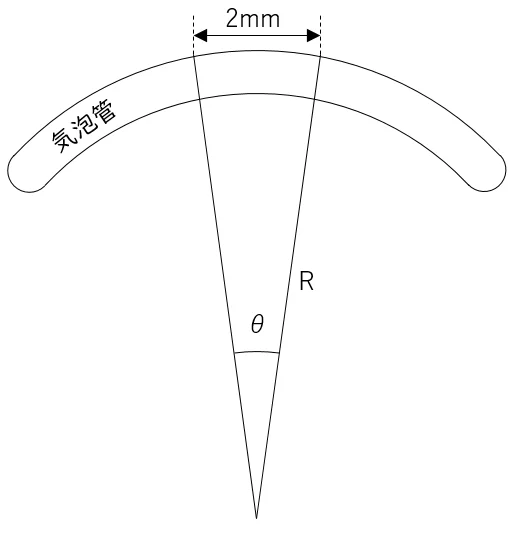
気泡管の感度は,気泡管上の2mmに対する中心角θで表される。曲率半径Rとの関係は,以下の式となる。
θ[rad]=2mm÷曲率半径R
また,θは微小角のため,ρ″をかけることで,度分秒に変換することができる。
θ=2mm÷曲率半径R×ρ″
問題文からθは32″のため,32″=2mm÷曲率半径R×ρ″となる。この式を変形すると,以下になる。
32″=2mm÷曲率半径R×ρ″
曲率半径R=2mm÷32″×ρ″
となり,単位をmに統一すると,以下になる。
曲率半径R=0.002m÷32″×2″×105
=12.5m
以上により,曲率半径は12.5mと求められた。
よって,正解は「3」である。
問2<距離の観測誤差>
距離の観測誤差の正誤問題である。
1 〇
器械定数及び反射鏡定数の誤差は定数であり,測定距離には比例しない。
2 〇
気象(気温・気圧・湿度)要素は,基準となる光の速度を変えてしまうことから,気象要素の測定誤差は測定距離に比例する。
3 〇
気圧が高くなり分子密度が高くなるほど光の速度が遅くなるため,実際の距離よりも観測距離は長くなる。
4 ×
気温が高くなり分子密度が低くなるほど光の速度が早くなるため,実際の距離よりも観測距離は短くなる。
5 〇
気温と気圧の変化が観測距離に与える影響では,気温の変化が与える影響の方が相対的に大きい。
よって,誤っているのは「4」である。
問3<閉合比>
結合多角方式により,方向角と閉合比を計算する問題である。
まずは,B点の方向角を求める。A点からP1,P1からP2,P2からB点,B点からD点と,順次方向角を求めていく。
なお,P2からB点の方向角は最後に調整するため,xに記憶させておく。
①A点からP1の方向角を求める
8°54°5°+176°29°50°=
②P1からP2の方向角を求める
Ans+93°25°49°=
Ans-180=
③P2からB点の方向角を求めてxに記憶させる
Ans+83°58°15°=
Ans-180→x
④B点からD点の方向角を求める
Ans+269°25°=
Ans-180=
以上により求まった観測値と,実際の92°12′55″との差が誤差となる。
この誤差を観測点数(4)で割り,調整量を求める。
①調整量を求める
92°12°55°-Ans=
Ans÷4=
求めるべきP2からB点の方向角の観測は観測点数3なので,調整量に3をかけ,xに加えることで調整後の方向角を計算する。
Ans×3+x=
以上により,調整後のP2からB点の方向角は2°47′56″と求められた。
次に,閉合比を求める。閉合比とは,閉合差と路線長の比であり,閉合差を路線長で割ることにより求める。
閉合差は問題に0.008mとあることから,閉合比は以下のように求められる。
閉合差=(109.402+115.245+120.617)÷0.008
分数の形式にすると,1/43158と求められた。
よって,正解は「2」である。
問4<座標計算>
まずは,A点とB点の座標値をそれぞれメモリ「A」と「B」に記憶させる。
①A点をAに記憶させる
-50522.6-15532.07i→A
②B点をBに記憶させる
-50481.27-15454.81i→B
求めるべき方位角は,方向角から真北方向角を引いたものとなる。
①AからBの方向角を求める
Arg(B-A=
②AからBの方位角を求める
Ans-0°2°=
以上により,A点からB点の方位角は61°49′20.1″と求められた。
次に,A点とB点の平面距離を求める。
①AからBの距離を求める
Abs(A-B=
以上により,A点からB点の平面距離は87.620…と求められた。
よって,正解は「2」である。
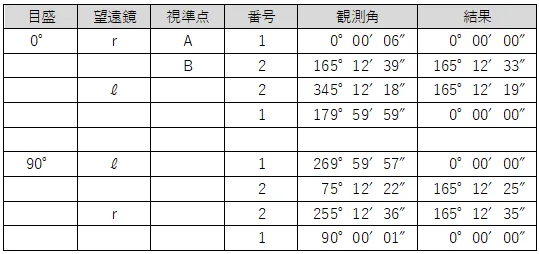
問5<観測手簿>
観測値から,高低角と高度定数の較差を計算する問題である。
まずは,各点の正反の鉛直角観測値をメモリに記憶させる。T1の正反をそれぞれ「A」,「B」に,T2の正反をそれぞれ「C」,「D」に,T3の正反をそれぞれ「E」,「F」に記憶させる。
①T1の正の観測値をAに記憶させる
90°42°31°→A
②T1の反の観測値をBに記憶させる
269°17°37°→B
③T2の正の観測値をCに記憶させる
84°0°34°→C
④T2の反の観測値をDに記憶させる
275°59°28°→D
⑤T3の正の観測値をEに記憶させる
88°53°38°→E
⑥T3の反の観測値をFに記憶させる
271°6°18°→F
高低角は,90°から鉛直角の最確値を引いたものになる。最確値は,観測された鉛直角を平均することで求められる。
なお,望遠鏡の反の観測値は360°から差し引くことに注意する。
①T1の鉛直角の最確値を求める
A+360-B=
Ans÷2=
②T1の高低角を求める
90-Ans=
以上により,T1の高低角は-0°42′27″と求められた。
①T2の鉛直角の最確値を求める
C+360-D=
Ans÷2=
②T2の高低角を求める
90-Ans=
以上により,T2の高低角は+5°59′27″と求められた。
①T3の鉛直角の最確値を求める
E+360-F=
Ans÷2=
②T3の高低角を求める
90-Ans=
以上により,T3の高低角は+1°6′20″と求められた。
次に,高度定数の較差を求めるため,各点の高度定数を求める。望遠鏡の正反の観測値の合計と360°との差が高度定数になる。
①T1の高度定数を求め,xに記憶させる
A+B-360→x
②T2の高度定数を求め,yに記憶させる
C+D-360→y
③T3の高度定数を求め,Mに記憶させる
E+F-360→M
最後に高度定数の較差を求める。高度定数の較差とは,一連の観測における高度定数の最大値と最小値の差である。
最大値はT1の高度定数(x)であり,最小値はT3の高度定数(M)である。
①高度定数の較差を求める
x-M=
以上により,高度定数の較差は0°0′12″と求められた。
よって,正解は「4」である。