測量士試験の写真測量の問題ですが，近年は令和２年３月31日の作業規程の準則の改正から，UAV（ドローン）による写真測量の問題も出題されるようになりました。

UAVだと，有人航空機よりもオーバーラップとサイドラップが大きくなるので，今までの解き方をちょっと変える必要が出てきました。そこで，汎用性の高い，どんな重複度でも解ける方法を考えました。

こんな撮影条件で考えてみましょう。この記事では，「最少撮影枚数」を導くために必要なものだけ書いてます。

①計測対象範囲は，東西18km，南北13kmの平たんな地域とする。
②デジタル航空カメラは，画面の大きさ17,310画素×11,310画素とし，画面の短辺は撮影基線と平行とする。
③撮影基準面における地上画素寸法は20cmとする。
④撮影基準面における同一撮影コース内の隣接写真との重複度を60％，隣接撮影コースの空中写真との重複度を30％とする。
⑤撮影コースは東西方向とする。
⑥南北両端の撮影コースでは，撮影区域外を画面の大きさの20％以上含むように撮影する。
⑦各撮影コースの両端は，撮影区域外に各1モデル分撮影する。

試験問題でよくある有人航空機の条件です。

まずは，「１枚の空中写真で撮影できる範囲（撮影範囲）」を求めてみましょう。

地上画素寸法が条件③から，水平格子間隔20cmとなってます。これが，デジタル航空カメラの画面の大きさの画素数だけ縦横に並ぶわけですから，条件②の画面の大きさ17,310画素×11,310画素を掛けてあげて，長辺が17,310×20cm＝3,462ｍで，短辺が11,310×20 cm＝2,262ｍが１枚の撮影範囲となります。

次に，「航行区域の短辺」を求めます。「航行区域」という用語はなく，中山の造語です。計測対象範囲に，範囲外の部分を加えた「航空機がカバーしなければならない範囲」を意味します。これを考えてあげることでぐっと分かりやすくなります。

通常は，最少コース数を求めるため，航行区域の短辺だけ考えてあげればよいです。長辺も考慮する必要がある場合は，後述します。

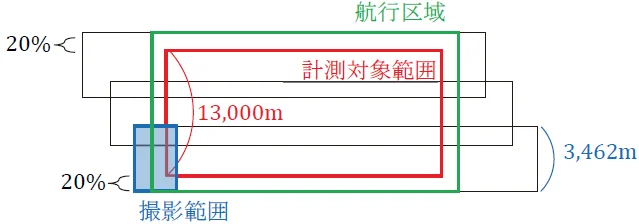
計測対象範囲の短辺（南北）は，条件①から13km＝13,000ｍですが，航行区域には，条件⑥から計測対象範囲の短辺の両端に撮影区域外を画面の大きさ（空中写真の撮影範囲の大きさの長辺）の20％以上含む必要があるため，航行区域の短辺は，13,000＋3,462×0.2×2＝14,384.8ｍとなります。20％を×2しているのは，両端に（2つ）含む必要があるからです。

図にするとこんな感じですね。

そして，この航行区域をカバーする「最少撮影コース数」を次に求めます。

航行区域の短辺（南北）が14,384.8ｍであり，撮影範囲の長辺（南北）が3,462ｍです。

コース数をNとおくと，Nコースあたりの撮影範囲は，条件④からサイドラップを30％とするため，3,462＋（N－1）×（3,462×0.7）ｍとなります。

もしコース数Nが1だったら，撮影範囲長辺の3,462ｍが撮影範囲になりますが，Nが1増えていくごとに，サイドラップしない部分（コース間の距離）が増えていくことになります。

なので，コース間の距離（3,462×0.7）を1コース目を除いたコース数（N－1）だけ，撮影範囲長辺の3,462ｍに加えています。

あとは，3,462＋（N－1）×（3,462×0.7）ｍが航行区域の短辺である14,384.8ｍを超えるNを求めてあげれば，それが最少撮影コース数となります。つまり，（14,384.8－3,462）÷（3,462×0.7）＋1を計算すればよいです。

計算すると，5.0507…となりますが，コース数は自然数（正の符号の整数）となるので，5.0507…以上の自然数である，6コースとなります。

最後に，「１コースあたりの撮影写真枚数」を求めて，最終的な「最少撮影枚数」をだしていきましょう。

まずは，写真の枚数の前にモデル数を考えます。

モデル間の距離（撮影基線長）は，条件④からオーバーラップを60％とするため，2,262×0.4＝904.8ｍとなります。これが計測対象範囲の長辺（東西）をカバーしていればよいので，計測対象範囲の長辺である18km＝18,000ｍを割ると，18,000÷904.8＝19.8938…となります。ですが，モデル数は自然数（正の符号の整数）となるので，19.8938…以上の自然数である，20モデルとなります。

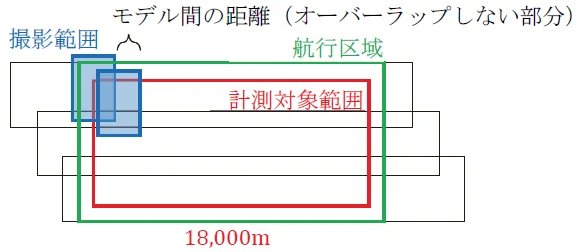
ただし，条件⑦に，「各撮影コースの両端は，撮影区域外に各1モデル分撮影する。」とありますから，両端に（2モデル）加えてあげる必要があるので，20＋2＝22モデルが，１コースあたりのモデル数となります。

モデルは写真の重複部分なので，例えば，１モデルつくるためには２枚の写真が必要になります。２モデルつくるためには３枚の写真，３モデルつくるためには４枚の写真が必要になるので，撮影写真枚数＝モデル数＋１になります。

１コースあたりのモデル数が22モデルなので，１コースあたりの撮影写真枚数は，22＋1＝23枚です。

あとは，最少撮影コース数が6コースなので，23×6＝138枚が最少撮影枚数。求めるべき答えになります！

いかがでしたでしょうか？

実は，撮影計画の問題には，もう一つバリエーションがあり，それは条件⑦が「各撮影コースの両端に，撮影される範囲のすべてが計測対象範囲の外となる写真を撮影する。」となっているものです。この場合，最少撮影コース数を求めるところまでは同じですが，１コースあたりの撮影枚数を求める方法が異なります。これは，航行区域の長辺をコース数を求めるように考えてあげればokです。

あまり出題されませんが（１回だけ出題されたことがあります。），一応やっておきましょう。条件⑦だけ変わります。最少コース数を求めるところまでは一緒です。

⑦各撮影コースの両端に，撮影される範囲のすべてが計測対象範囲の外となる写真を撮影する。

まず，「航行区域の長辺」を求めます。

計測対象範囲の長辺（東西）は，条件①から18km＝18,000ｍですが，航行区域には，条件⑦から計測対象範囲の長辺の両端に撮影区域外を画面の大きさ（空中写真の撮影範囲の大きさの短辺）のすべてを含む必要があるため，航行区域の長辺は，18,000＋2,262×2＝22,524ｍとなります。撮影範囲の短辺を×2しているのは，両端に（2つ）含む必要があるからです。

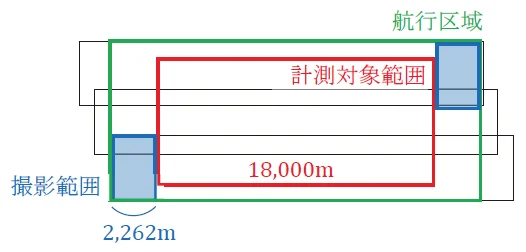
そして，この航行区域の長辺をカバーする「最少撮影枚数」を求めていきます。

航行区域の長辺（東西）が22,524ｍであり，撮影範囲の短辺（東西）が2,262ｍです。

撮影枚数をNとおくと，N枚あたりの撮影範囲は，条件④からオーバーラップを60％とするため，2,262＋（N－1）×（2,262×0.4）ｍとなります。

もし撮影枚数Nが1だったら，撮影範囲短辺の2,262ｍが撮影範囲になりますが，Nが1増えていくごとに，オーバーラップしない部分（モデル間の距離・撮影基線長）が増えていくことになります。

なので，モデル間の距離（2,262×0.4）を1枚目を除いた枚数（N－1）だけ，撮影範囲短辺の2,262ｍに加えています。

あとは，2,262＋（N－1）×（2,262×0.4）ｍが航行区域の長辺である22,524ｍを超えるNを求めてあげれば，それが１コースあたりの最少撮影枚数となります。つまり，（22,524－2,262）÷（2,262×0.4）＋1を計算すればよいです。

計算すると，23.3938…となりますが，撮影枚数は自然数（正の符号の整数）となるので，23.3938…以上の自然数である，24枚が，１コースあたりの撮影写真枚数となります。

あとは，最少撮影コース数が変わらず6コースなので，24×6＝144枚が最少撮影枚数。求めるべき答えです。

モデル数を２つ余計に取るか，写真を２枚余計に撮るかで，最少撮影枚数が異なってきます。

ここまでできれば完璧ですね。

それでは！