測量士補の計算問題は10/28問以上出題されますので，まったく計算問題を解かずに合格というのは難しいです。
なので，得意な計算問題をストックしていくような学習をしていきましょう。

今日は，測量士補の計算問題の裏ワザについてです。
測量士試験や調査士試験と異なり，測量士補には記述式問題がありません。
なので，計算問題も答えが５択のどこかに書かれています。ここがポイントなんです。

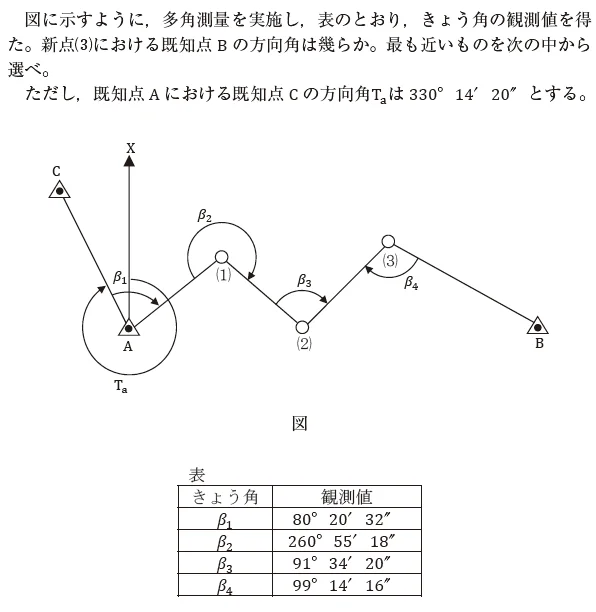
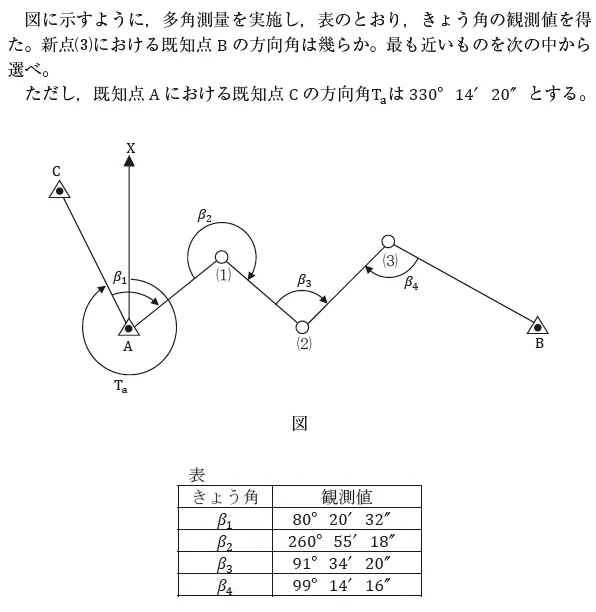
例えば，長い計算が連続する，この多角測量の方向角の問題（H25問6）をみてみましょう。

１　　123° 50′ 14″
２　　133° 04′ 45″
３　　142° 18′ 46″
４　　172° 04′ 26″
５　　183° 21′ 34″

この５つの中に正解があるってのがポイントです。
どういうことでしょうか？

普通に計算すると，以下のようになります。

点A における点⑴の方向角①
①＝Ta＋𝛽1－360°
　＝330°14′20″＋80°20′32″－360°
　＝50°34′52″

点⑴における点⑵の方向角②
②＝①＋𝛽2－180°
　＝50°34′52″＋260°55′18″－180°
　＝131°30′10″

点⑵における点⑶の方向角③
③＝②＋𝛽3－180°
　＝131°30′10″＋91°34′20″－180°
　＝43°4′30″

点⑶における点B の方向角④
④＝③＋180°－ 𝛽4
＝43°4′30″＋180°－ 99°14′16″
＝123°50′14″

これで，答えが肢１と計算することができます。
でも，ちょっと考えてみてください。答えは５つのどれかですよ？
ということは，実は「秒の位だけ計算すればよい」ということになります。

秒の値が求まれば，あとはその秒を選択肢の中から探せばいいんです。
そうすると，60進数を考える回数が圧倒的に少なくなりますし，度と分が無視できるので，「－360°」とか「－180°」とか不要です。

ちょっとやってみましょう。

点A における点⑴の方向角①の秒
①＝20″＋32″＝52″

点⑴における点⑵の方向角②の秒
②＝①＋18″＝70″＝10″

点⑵における点⑶の方向角③の秒
③＝②＋20″＝30″

点⑶における点B の方向角④の秒
④＝③－16″＝14″

とても簡単になりません？筆算で考えたら違いは歴然です。
あとは選択肢の中から「14″」のものを選ぶだけです。
H30の問題ではちょっと対策がされて同じ秒の選択肢が２つありますが，この場合でも，「分まで」計算してあげれば，「－360°」とか「－180°」とか不要になるので早くなります。

方向角の他にも，高低角や高度定数，座標計算などなどの角度全般だけでなく，基線ベクトルや偏心補正，重量平均なんかでも「答えが書いてあるから」できる省略や裏ワザがあったりします。

応用が効かないんで積極的に教えることはありませんが，こういうの見つけると復習時間も短縮できますね！


それでは！