問６＜座標計算＞

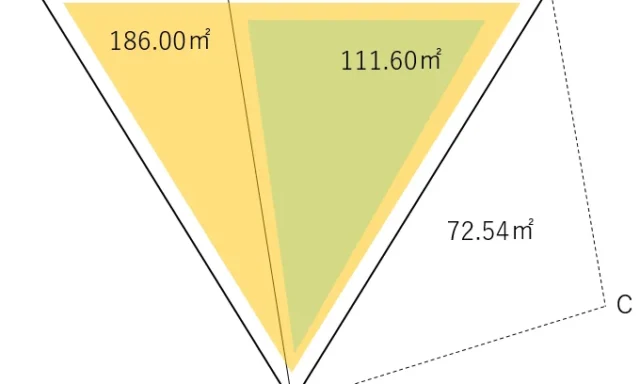
水平角βを求めるため，Ｐ点の座標値を求める。
まずは，T1，T2，T3をそれぞれメモリ「Ａ」，「Ｂ」，「Ｃ」に記憶させる。

①T1をＡに記憶させる
89.55＋122.5ｉ→Ａ

②T2をＢに記憶させる
93.72＋127.47ｉ→Ｂ

③T3をＣに記憶させる
90.12＋116.6ｉ→Ｃ

T2を後視としたT1からＰ点までの観測角と距離から，Ｐ点の座標値を求める。

①T1からT2の方向角を求める
Arg(Ｂ－Ａ＝

②Ｐ点の座標値を求め，Ｄに記憶させる
Ａ＋5.15∠(Ans＋299→Ｄ

次に，T3からＰ点の方向角から，T3からT2の方向角を引き，水平角βを求める。

①T3からＰ点の方向角を求める
Arg(Ｄ－Ｃ＝

②T3からT2の方向角を引き，水平角を求める
Ans－Arg(Ｂ－Ｃ＝
Ans＋360＝

以上により，水平角βは335°57′19.26″と求められた。
よって，正解は「４」である。

問７＜GNSS測量における注意点＞

GNSS測量における注意点に関する正誤問題である。

１　×
スタティック法による観測のみ，GPS及び準天頂衛星を同時に４衛星以上使用しなければならず，ネットワーク型RTK法を含むスタティック法以外の観測法では，GPS及び準天頂衛星を同時に５衛星以上使用しなければならない。

２　×
GPSが地球全体をカバーするように地球を周回するのに対し，準天頂衛星は日本を中心としたアジア・オセアニア地域での利用に特化した軌道をもつ。

３　×
準天頂衛星の軌道は南北非対称の８の字となり，北半球に約13時間、南半球に約11時間留まり、日本付近に長く留まるよう設計されている。

４　〇
地心直交座標の座標値の計算によっても，準拠楕円体（GRS80）からの高さである楕円体高までしか求めることはできず，標高を直接測ることはできない。そのため，国土地理院が提供するジオイドモデルより求めたジオイド高を楕円体高から差し引くことで標高を得る必要がある。

５　×
マルチパスとは，衛星から直接到達する電波以外に電波が構造物などに当たって反射したものが受信される現象のことで，雑電波となり誤差の原因となる。マルチパスの影響は周波数に依存せず，２周波の観測により軽減することができない。

よって，正しいものは「４」である。

問８＜地図の投影法＞

地図の投影法に関する正誤問題である。

ア　×
平面直角座標系もUTM図法と同じく，正角横円筒図法のガウス・クリューゲル図法で描かれている。

イ　×
日本全国を19の地域に分けて範囲を定義しており，それぞれの座標系原点の経緯度を定義している。

ウ　×　／　オ　〇
縮尺係数はＸ軸において0.9999，東西に約90km離れたところで1.0000である。よって，Ｘ座標値が同じであっても，Ｙ座標値の違いによって縮尺係数が異なる。

エ　〇
座標系のＸ軸は座標系原点において子午線に一致する軸とし，真北に向かう値を正（＋）とする。また，座標系のＹ軸は，座標系原点において座標系のＸ軸に直交する軸とし，真東に向かう値を正（＋）とする。

よって，正しいものはエ，オであり，その組合せは「５」である。

問９＜重量平均による最確値＞

観測値から，重量平均による最確値を計算する問題である。

各路線におけるＥの標高を求めて，メモリ「Ａ」から「Ｄ」に記憶させる。

①Ａ→Ｅの標高を求めてＡに記憶させる
7.13－3.125→Ａ

②Ｂ→Ｅの標高を求めてＢに記憶させる
3.659＋.329→Ｂ

③Ｅ→Ｃの標高を求めてＣに記憶させる
3.139＋.873→Ｃ

④Ｅ→Ｄの標高を求めてＤに記憶させる
6.708－2.709→Ｄ

重量は路線長に反比例することから，各路線の観測距離から重量を求める。
　Ｅ→Ａの重量：Ｅ→Ｂの重量：Ｃ→Ｅの重量：Ｄ→Ｅの重量
　　＝1/3：1/4：1/1：1/2＝4/12：3/12：12/12：6/12
　　＝4：3：12：6

最後に，重量平均による最確値を求める。

①重量平均による最確値を求める
Ａ×4＋Ｂ×3＋Ｃ×12＋Ｄ×6＝
Ans÷(4＋3＋12＋6)＝

以上により最確値は，4.00488ｍと求められた。
よって，正解は「３」である。

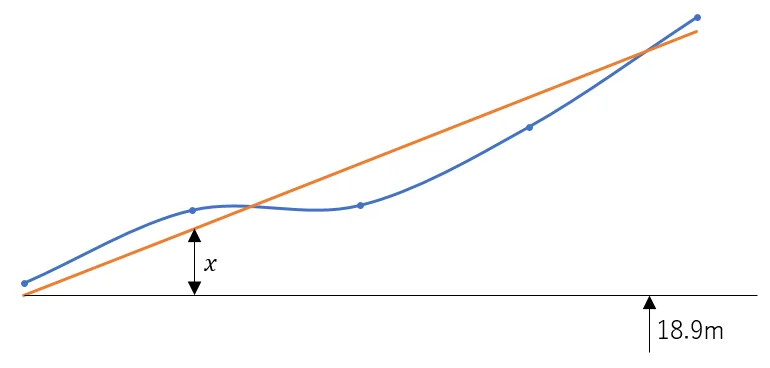
問10＜縦断測量＞

勾配のある計画道路の切土量を計算する問題である。

No.1の計画道路の高さが18.9ｍであり，各測点は18ｍ間隔で上り勾配は1.5％である。
まずは，前の測点との比高を計算し，メモリ「ｘ」に記憶させる。

①前の測点との比高を求め，ｘに記憶させる
18×0.015→ｘ

①No.1の計画道路の高さをＡに記憶させる
18.9→Ａ

②No.2の計画道路の高さを求め，Ｂに記憶させる
Ans＋ｘ→Ｂ

③No.3の計画道路の高さを求め，Ｃに記憶させる
Ans＋ｘ→Ｃ

④No.4の計画道路の高さを求め，Ｄに記憶させる
Ans＋ｘ→Ｄ

⑤No.5の計画道路の高さを求め，Ｅに記憶させる
Ans＋ｘ→Ｅ

次に，各測点の切土量（現況の高さ－計画道路の高さが＋になる量）を求める。

①No.1の切土量を求める
18.95－Ａ＝

②No.2の切土量を求める
19.25－Ｂ＝

③No.3の切土量を求める
19.27－Ｃ＝

④No.4の切土量を求める
19.59－Ｄ＝

⑤No.5の切土量を求める
20.04－Ｅ＝

以上により，切土量がもっとも大きいのは，No2の＋0.08ｍと求められた。
よって，正解は「２」である。

▲まとめ に戻る！▲