問６＜偏心計算＞

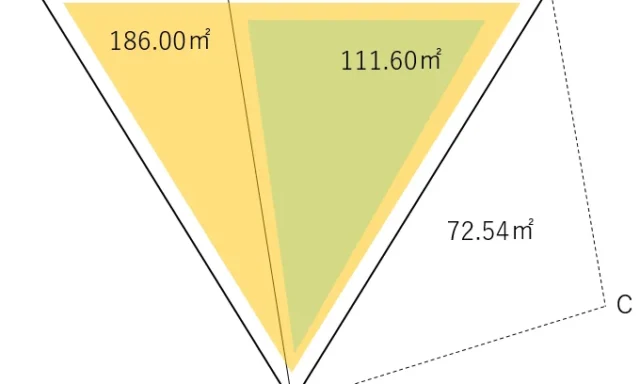
Ａ点の座標値をＸ座標100Ｙ座標100とし，Ａ点からＣ点の方向角を90度としたときのＢ点とＣ点の座標値を求める。

①Ａ点をＡに記憶させる
100＋100ｉ→Ａ

②Ｃ点の座標値を求め，Ｃに記憶させる
Ａ＋100∠90→Ｂ

③ＣからＡの方向角を求める
Arg(Ａ－Ｃ

③Ｂ点の座標値を求め，Ｂに記憶させる
Ｃ＋1000∠(Ans－240→Ｂ

以上によりＢ点の座標値が求められた。
最後に，Ａ点からＢ点の距離を求める。

①Ａ点からＢ点の距離を求める
Abs(Ａ－Ｂ＝

以上によりＡ点からＢ点の距離は，1053.565…と求められた。
よって，正解は「３」である。

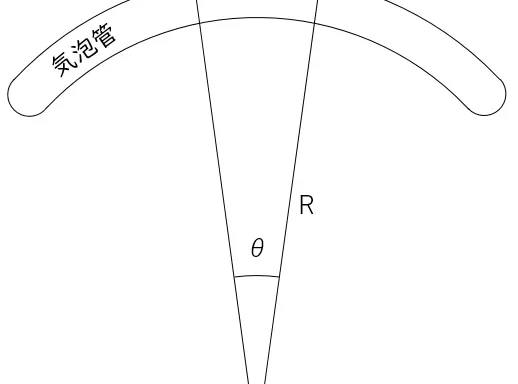
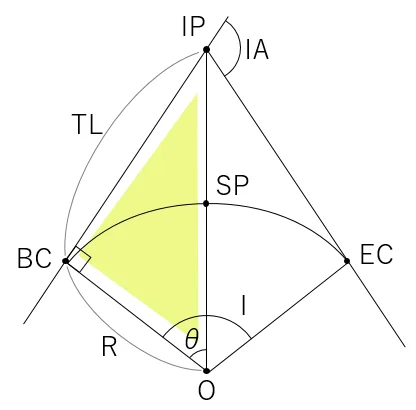
問７＜単曲線の設置（計画変更）＞

計画変更による単曲線の設置を計算する問題である。

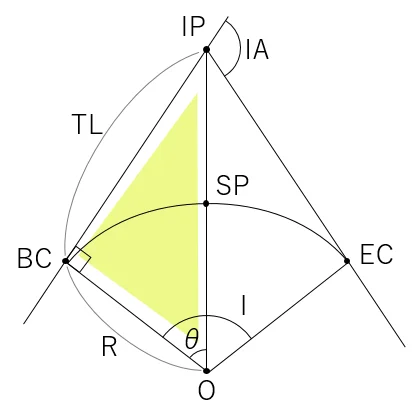
変更前と変更後のTL（接線長）は等しく，IA（交角）とI（中心角）は等しくなるという図形的特徴がある。

変更前のIAは68°であるため，Iも68°となり，図中のθは68÷2＝34°となる。
三角形ABDは直角三角形であり，三角関数から，TL＝tanθ×Ｒとなる。なお，Ｒ（曲線半径）は，問題文から400ｍである。

①TLを求める
tan(34)×400＝

変更後のIAは，68＋12＝80°であるため，Iも80°となり，図中のθは80÷2＝40°となる。
同様に，三角形FBDも直角三角形であるから，三角関数から，Ｒ＝TL÷tanθとなる。

②変更後のＲを求める
Ans÷tan(40＝

最後に，半径Ｒ，中心角80°の弧の長さを計算することで，単曲線BEの距離が求められる。

③単曲線BEの距離を求める
Ans×2×3.14×80÷360＝

以上により単曲線BEの距離は，448.725…と求められた。
よって，正解は「５」である。

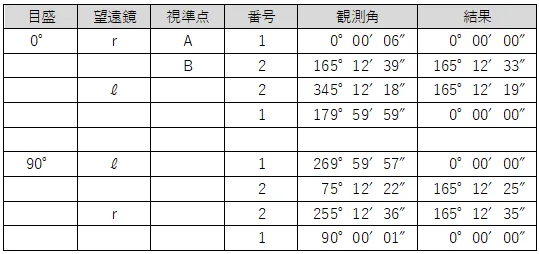
問８＜観測手簿（水平角）＞

観測値から，水平角を計算する問題である。

まずは，「結果」を計算する。
結果は，新点（Ｂ・Ｃ）の観測角から基準となる点（Ａ）の観測角を引くことで計算する。

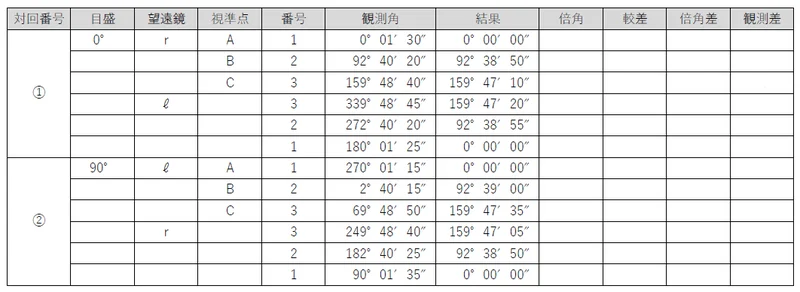
次に，対回ごとに，新点の結果について正反の合計を計算する。この値を「倍角」という。
通常は，秒の単位だけ合計すれば足りる。
さらに，新点の結果について正（ｒ）の結果から反（ℓ）の結果を引く。この値を「較差」という。

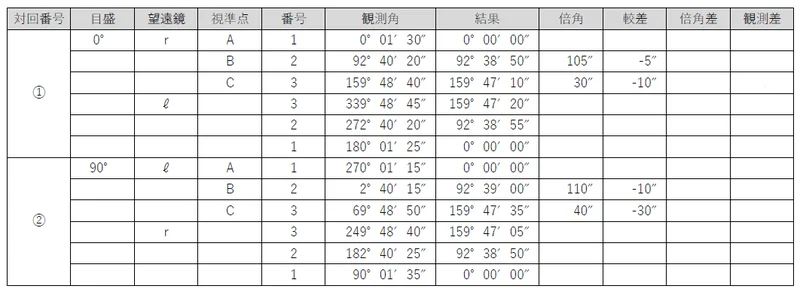
最後に，それぞれの対回の組合せごとの「倍角差」と「観測差」を計算する。
「倍角差」は，倍角の最大値から最小値を引くことで求められ，「観測差」は，較差の最大値から最小値を引くことで求められる。

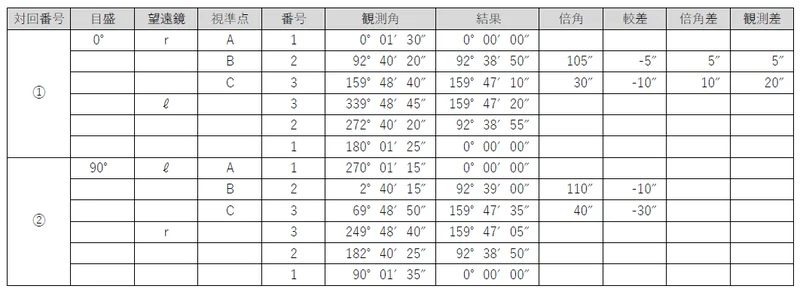
許容値は，問題文から倍角差25″，観測差15″なので，Ｃ方向の観測差のみが制限を超えている。
よって，正解は「４」である。

問９＜座標計算＞

まずは，A101，A102，Ｐ点をそれぞれメモリ「Ａ」，「Ｂ」，「Ｃ」に記憶させる。

①A101をＡに記憶させる
-10200.07＋1205.83ｉ→Ａ

②A102をＢに記憶させる
-10196.83＋1219.35ｉ→Ｂ

③Ｐ点をＣに記憶させる
-10199.79＋1192.94ｉ→Ｃ

次に，A101からＰ点の方向角から，A101からA102の方向角を引き，水平角を求める。

①A101からＰ点の方向角を求める
Arg(Ｃ－Ａ＝
Ans＋360＝

②A101からA102の方向角を引き，水平角を求める
Ans－Arg(Ｂ－Ａ＝

以上により，A102を後視としたA101からＰ点までの水平角は194°43′15.23″と求められた。
最後に，A101からＰ点までの距離を求める。

①A101からＰ点までの距離を求める
Abs(Ａ－Ｃ＝

以上により，A101からＰ点までの距離は12.893…ｍと求められた。
よって，正解は「５」である。

問10＜均等法によるトラバース調整＞

Ａ点からＣ点までの観測角と距離から，観測されたＣ点（CD）の座標値を求める。
まずは，Ａ点，Ｂ点，Ｃ点を，それぞれメモリ「Ａ」，「Ｂ」，「Ｃ」に記憶させる

①Ａ点をＡに記憶させる
2076.13＋1428.66ｉ→Ａ

②Ｂ点をＢに記憶させる
2186.91＋1539.44→Ｂ

③Ｃ点をＣに記憶させる
2301.56＋1701.56ｉ→Ｃ

順次，放射計算により座標値を求めていく。

①Ｂ点からＡ点を後視にし，方向角と距離でＰ点の座標値を求め，Ｄに記憶させる
Arg（Ａ－Ｂ＝
Ｂ＋49.55∠(Ans＋225→Ｄ

②Ｐ点からＢ点を後視にし，方向角と距離でＱ点の座標値を求め，Ｅに記憶させる
Arg（Ｂ－Ｄ＝
Ｄ＋52.09∠(Ans＋90→Ｅ

②Ｑ点からＰ点を後視にし，方向角と距離でＲ点の座標値を求め，Ｆに記憶させる
Arg（Ｄ－Ｅ＝
Ｅ＋50.01∠(Ans＋270→Ｆ

③Ｒ点からＱ点を後視にし，方向角と距離でCDの座標値を求め，Ｍに記憶させる
Arg（Ｅ－Ｆ＝
Ｆ＋88.36∠(Ans＋135→Ｍ

Ｃ点の座標値からCDの座標値を引くことで，補正量を求める。

④補正量を求める
Ｃ－Ｍ＝

均等法では観測数で調整することとなるため。補正量を観測数の合計で割り，それに求める観測点（Ｑ点）までの観測数をかけて調整誤差を計算する。その調整誤差を観測結果に足すことで，最確値を求めることができる。

⑤均等法による閉合調整をする
Ans÷4×2＝

⑥Ｑ点を調整する
Ans＋Ｅ＝

以上により，調整後のＱ点の座標値は，Ｘ座標2239.040…Ｙ座標1589.030…と求められた。
よって，正解は「４」である。

▲まとめ に戻る！▲