問11　小問１＜コンパス法によるトラバース調整＞

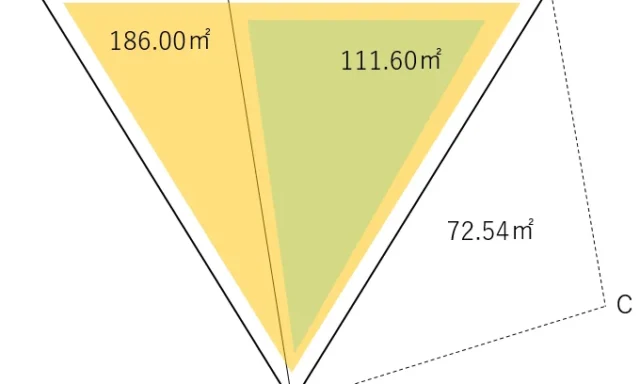
T1からT4までの観測角と距離から，観測されたT4（T4D）の座標値を求める。
まずは，T1，T2，T4を，それぞれメモリ「Ａ」，「Ｂ」，「Ｄ」に記憶させる。

①T1をＡに記憶させる
528.65＋472ｉ→Ａ

②T2をＢに記憶させる
498.72＋475.95→Ｂ

③T4をＤに記憶させる
526.39＋528.67ｉ→Ｄ

順次，放射計算により座標値を求めていく。

①T2からT1を後視にし，方向角と距離でT3の座標値を求め，Ｃに記憶させる
Arg（Ａ－Ｂ＝
Ｂ＋20∠(Ans＋60°4°31°→Ｃ

②T3からT2を後視にし，方向角と距離でT4Dの座標値を求め，Ｍに記憶させる
Arg（Ｂ－Ｃ＝
Ｃ＋40∠(Ans＋194°37°40°→Ｍ

T4の座標値からT4Dの座標値を引くことで，補正量を求める。

③補正量を求める
Ｄ－Ｍ＝

コンパス法では各辺長で調整することとなるため。補正量を観測辺長の合計で割り，それに求める観測点（T4）までの辺長の合計をかけて調整誤差を計算する。その調整誤差を観測結果に足すことで，最確値を求めることができる。

④コンパス法による閉合調整をする
Ans÷(20＋40)×20＝

⑤T3を調整する
Ans＋Ｃ＝

以上により，調整後のT3の座標値は，Ｘ座標510.879…Ｙ座標491.819…と求められた。
よって，値を四捨五入し，正解はＸ座標「510.88」Ｙ座標「491.82」である。

問11　小問２＜交点計算＞

２直線の交点の座標を求める問題である。

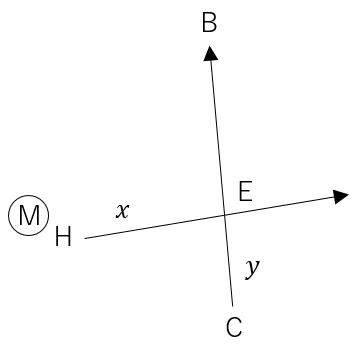
Ｅ点は，Ｈ点から方向角60°の直線と，ＢＣを結んだ直線の交点となる。交点計算をする場合は，下のようなメモを書く。

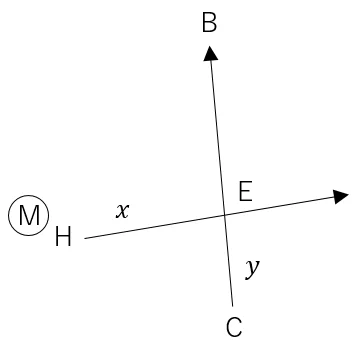
交点計算に必要なＢ，Ｃ，Ｈ点を，それぞれメモリ「Ｂ」，「Ｃ」，「Ｍ」に記憶させる。

①Ｂ点をＢに記憶させる
532.05＋494.23ｉ→Ｂ

②Ｃ点をＣに記憶させる
514＋494.23ｉ→Ｃ

③Ｈ点をＭに記憶させる
505.73＋476.91ｉ→Ｍ

Ｈ点からの方向角を「ｘ」に，ＣからＢの方向角を「ｙ」に記憶させる。

①Ｈ点からの方向角をｘに記憶させる
60→ｘ

②ＣからＢの方向角を求め，ｙに記憶させる
Arg(Ｂ－Ｃ→ｙ

③方向角ｘを加工して，ｘに記憶させなおす
tan(ｘ)＋ｉ→ｘ

④方向角ｙを加工して，ｙに記憶させなおす
tan(ｙ)＋ｉ→ｙ

⑤交点ＥのＸ座標を求めて，Ｅに記憶させる
Ｍｘ－Ｃｙ＝
Ans÷(ｘ－ｙ＝
ReP(Ans→Ｅ

実部を抽出し，「Ｅ」に記憶させた。この値が交点ＥのＸ座標となる。

⑥交点ＥのＹ座標を求めて，Ｅに記憶させる
Ans－Ｍ＝
Ans×ｘ＝
ReP(Ans)ｉ＋Ｅ→Ｅ

⑦Ｅ点の座標値を四捨五入し，Ｅに上書きする
515.73＋494.23ｉ→Ｅ

以上によりＥ点の座標値は，Ｘ座標515.73，Ｙ座標494.23と求められた。
よって，正解は，Ｘ座標「515.73」，Ｙ座標「494.23」である。

問11　小問３＜隅切り計算＞

Ａ，Ｈ，Ｅ点の座標値から∠AHEを求める。
まずは，Ａ点をメモリ「Ａ」に記憶させる。

①Ａ点をＡに記憶させる
529＋476.91ｉ→Ａ

次に，Ｈ点からＥ点の方向角から，Ｈ点からＡ点の方向角を引き，∠AHEを求める。

④ＨからＥの方向角を求める
Arg(Ｅ－Ｍ＝

⑤∠AHEを求め，ｘに記憶させる
Ans－Arg(Ａ－Ｍ→ｘ

求めるべきＨＦの距離は，ＧＦの距離（3ｍ）の半分をsin(ｘ/2)で割ったものとなる。

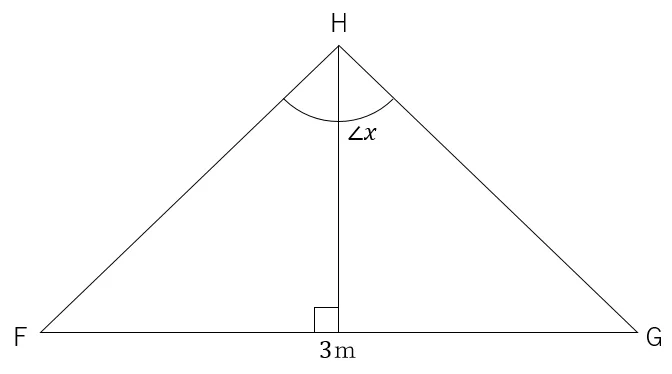
①ＨＦの距離を求め，ｙに記憶させる
sin(ｘ÷2＝
3÷2÷Ans→ｙ

最後に，Ｈ点からＥ点の方向にｙｍ移動させたＦ点の座標値を求める。

①ＨからＥの方向角を求める
Arg(Ｅ－Ｍ＝

②ＨからＥの方向にｙｍ移動させたＦの座標値を求め，Ｆに記憶させる
Ｍ＋ｙ∠Ans→Ｆ

③Ｆ点の座標値を四捨五入し，Ｆに上書きする
507.23＋479.51ｉ→Ｆ

以上によりＦ点の座標値は，Ｘ座標507.23，Ｙ座標479.51と求められた。
よって，正解は，Ｘ座標「507.23」，Ｙ座標「479.51」である。
なお，小問４と小問５で使用するため，Ｇ点の座標値も求めておく。Ｇ点は，Ｈ点からＡ点の方向にｙｍ移動させた座標値である。

①ＨからＡの方向角を求める
Arg(Ａ－Ｍ＝

②ＨからＡの方向にｙｍ移動させたＧの座標値を求め，ｘに記憶させる
Ｍ＋ｙ∠Ans→ｘ

③Ｇ点の座標値を四捨五入し，ｘに上書きする
508.73＋476.91ｉ→ｘ

以上によりＧ点の座標値は，Ｘ座標508.73，Ｙ座標476.91と求められた。

問11　小問４＜求積＞

本件拡幅地を構成する座標値であるＤ点を，メモリ「Ｄ」に記憶させる。

①Ｄ点をＤに記憶させる
504＋476.91ｉ→Ｄ

②求積をおこなう
Conjg(ｘ)Ｆ＋Conjg(Ｆ)Ｅ＋Conjg(Ｅ)Ｃ＋Conjg(Ｃ)Ｄ＋Conjg(Ｄ)Ｍ＋Conjg(Ｍ)ｘ＝
Ans÷2＝
ImP(Ans＝

以上により土地の面積は，33.8536と求められた。
よって，小数点以下第３位を切り捨て，正解は「33.85㎡」となる。

問11　小問５＜作図＞

（省略）
縮尺，方位，点名，辺長の記載をする他，本件元地と本件拡幅地に接する道路についても作図することに注意する。

▲まとめ に戻る！▲