問６＜点検計算＞

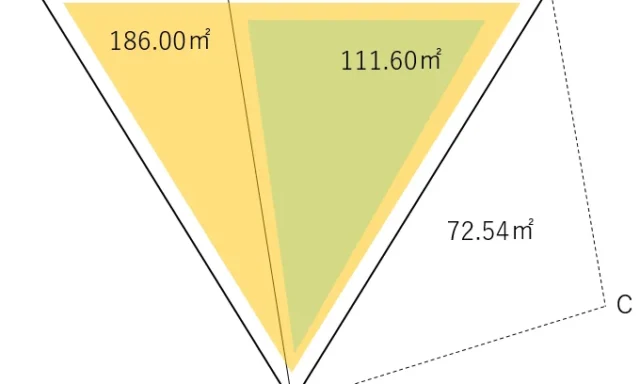
観測値から較差を計算し，再測の判断をする問題である。

まずは，再測すべき区間を決めるため，各区間の較差（往復の観測値の絶対値の差）を求める。

　①の較差＝0.2760－0.2765＝0.0005ｍ＝0.5mm
　②の較差＝1.1867－1.1842＝0.0025ｍ＝2.5mm
　③の較差＝1.2129－1.2107＝0.0022ｍ＝2.2mm
　④の較差＝0.6238－0.6233＝0.0005ｍ＝0.5mm

往復観測値の較差の許容範囲は，2.5mm√S kmであり，各区間の距離は640ｍ（0.64km）であるから，許容範囲は以下のように計算できる。

　0.64km区間の較差の許容範囲＝2.5mm√0.64
　　　　　　　　　　　　　　＝2.0mm

よって，②と③の区間の較差が許容範囲を超えているため，再測すべきと考えられる。
次に，再測すべき観測方向を求める。

往方向の高低差は，0.2760－1.1867－1.2129＋0.6233＝－1.5003ｍとなり，復方向の高低差は，－0.2765＋1.1842＋1.2107－0.6238＝1.4946ｍとなる。
問題文から，ＡＢ間の高低差は－1.5000ｍであるから，往方向では0.3mm，復方向では5.4mmの閉合差がある。

往復観測値の較差の許容範囲は，2.5mm√S kmであり，路線全体の距離は2560ｍ（2.56km）であるから，許容範囲は以下のように計算できる。

　路線全体の較差の許容範囲＝2.5mm√2.56
　　　　　　　　　　　　　＝4.0mm

よって，復方向の較差が許容範囲を超えているため，再測すべきと考えられる。
以上により，再測すべきと考えられる区間番号は②と③であり，再測すべきと考えられる観測方向は復方向であるから，その組合せは「５」である。

問７＜図形＞

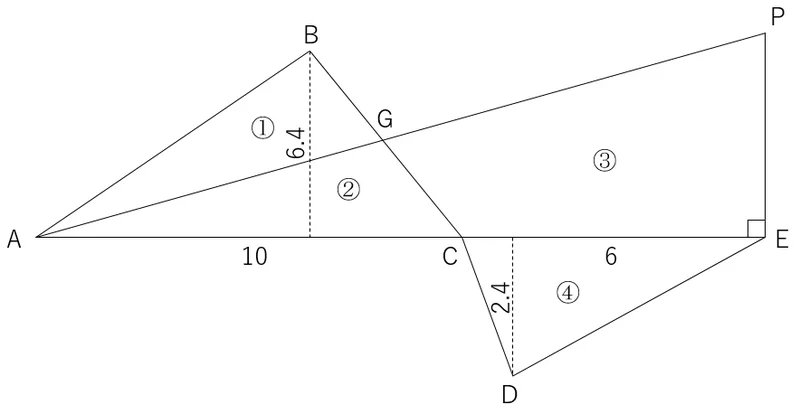
図を以下のように①から④の４つの部分で考える。

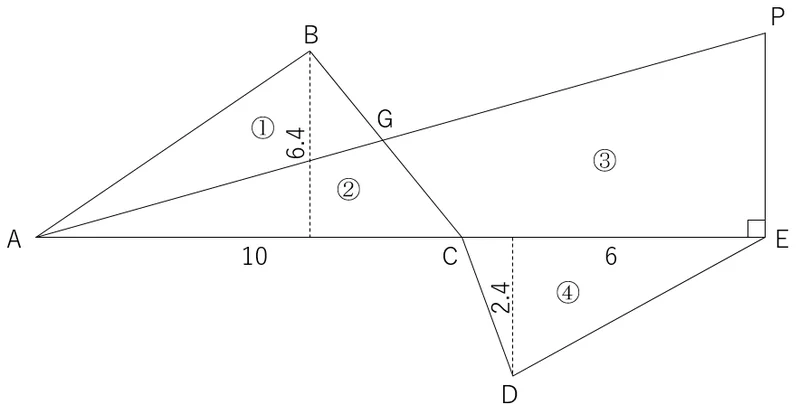
三角形ABC（①＋②）の面積は，AC×h1÷2から，10×6.4÷2＝32㎡となる。
また，三角形CDE（④）の面積は，CE×h2÷2から，6×2.4÷2＝7.2㎡となる。

三角形ABG（①）と五角形GCDEP（③＋④）が等しくなる距離PEを求めればよいことから，以下の式が導ける。

　①＝③＋④

左辺である①は，三角形ABC（①＋②）の面積（32㎡）から②を引いたものであり，右辺である③＋④は，三角形CDE（④）の面積（7.2㎡）に③を加えたものである。よって，式は以下のように変形できる。

　32－②＝7.2＋③
　32－7.2＝③＋②
　24.8＝③＋②

つまり，三角形APE（③＋②）が24.8㎡となる距離PEを求めればよい。
三角形APEの底辺は，h1＋h2から，10＋6＝16ｍであるので，24.8×2÷16＝3.1ｍとなる。

以上により距離PEは，3.1ｍと求められた。
よって，正解は「２」である。

問８＜重量平均による最確値（水平角）＞

観測値から，重量平均による最確値を計算する問題である。

重量は標準偏差の二乗に反比例することから，各観測の重量を求める。
　観測値87°26′40″の重量：観測値87°26′33″の重量
　　＝1/2²：1/5²＝1/4：1/25＝25/100：4/100
　　＝25：4

重量平均による最確値は，各観測結果の水平角が87°26′まで等しいと考えると，次の計算で求めることができる。
　最確値＝87°26′＋(40″×25＋33″×4)÷(25＋4)
　　　　＝87°26′＋1132″÷29
　　　　＝87°26′＋39.034…″
　　　　＝87°26′39.034…″

以上により水平角の最確値は，87°26′39.034…″と求められた。
よって，正解は「５」である。

問９＜方向角計算（閉合差）＞

観測値から方向角を計算し，閉合差を計算する。

Ａ点からP1，P1からP2，P2からP3，P3からＢ点，Ｂ点からＱ点と，順次方向角を求めていく。

①Ａ点からP1の方向角を求める
298°25°50°＋105°40°10°＝
Ans－360＝

②P1からP2の方向角を求める
Ans＋224°50°50°＝
Ans－180＝

③P2からP3の方向角を求める
Ans＋128°0°40°＝
Ans－180＝

④P3からＢ点の方向角を求める
Ans＋257°20°30°＝
Ans－180＝

⑤Ｂ点からＱ点の方向角を求める
Ans＋112°30°20°＝
Ans－180＝

以上により求まった観測値と，実際の46°48′10″との差が閉合差となる。

⑥閉合差を求める
Ans－46°48°10°＝

以上により，閉合差は10″と求められた。
よって，正解は「１」である。

問10＜座標計算＞

まずは，Ｔ点，Ａ点，Ｂ点をそれぞれメモリ「ｘ」，「Ａ」，「Ｂ」に記憶させる。

①Ｔ点をｘに記憶させる
100＋100ｉ→ｘ

②Ａ点をＡに記憶させる
115＋116ｉ→Ａ

③Ｂ点をＢに記憶させる
111＋117ｉ→Ｂ

Ｔ点からの方向角と距離により，放射計算でＰ点の座標値を求める。

①Ｐ点の座標値を求め，ｙに記憶させる
ｘ＋20.05∠50→ｙ

次に，Ｐ点からＡ点，Ｂ点の距離を求める。

①Ｐ点からＡ点の距離を求める
Abs(Ａ－ｙ＝

②Ｐ点からＢ点の距離を求める
Abs(Ｂ－ｙ＝

以上により，Ｐ点からＡ点の距離は2.207…ｍ，Ｐ点からＢ点の距離は2.501…ｍと求められた。
よって，正解は「１」である。

▲まとめ に戻る！▲