問１＜GNSS測量における注意点＞

GNSS測量における注意点に関する正誤問題である。

ア　〇
基線解析では，基線解析ソフトウェアで採用している標準値を用いて近似的に補正をおこなう。標準値を用いるため，観測点において測定した気温及び気圧の値を用いた気象補正は不要となる。よって，GNSS測量においては，通常，気温や気圧の気象観測はおこなわない。

イ　〇
電離層の影響は特に10km以上の長距離基線の場合影響があるため，周波数の異なる２周波（L1帯とL2帯）を受信できるGNSS受信機を使用し，２周波で基線解析を行う必要がある。

ウ　×
多角測量では基準点の座標がなければ新点の座標が求まらないように，GNSS測量では，衛星の軌道情報は観測方法にかかわらず解析作業には不可欠となる。

エ　×
地心直交座標の座標値の計算によっても，準拠楕円体（GRS80）からの高さである楕円体高までしか求めることはできず，標高を直接測ることはできない。そのため，国土地理院が提供するジオイドモデルより求めたジオイド高を楕円体高から差し引くことで標高を得る必要がある。

オ　〇
アンテナの位相特性による誤差の軽減のため，アンテナの向きは各点でそろえて整置する。

よって，誤っているものはウ，エであり，その組合せは「４」である。

問２＜逆計算＞

距離ＡＰとＢＰを用いた逆計算により座標値を求めることになる。

まずは，Ａ点とＢ点をそれぞれメモリ「Ａ」と「Ｂ」に記憶させる。

①Ａ点をＡに記憶させる
0＋0ｉ→Ａ

②Ｂ点をＢに記憶させる
40＋20ｉ→Ｂ　

Ａ点，Ｂ点及びＰ点をつなぐ三角形と見た場合，辺長ＡＰと辺長ＢＰは問題文の通りであるが，辺長ＡＢが不明なため，ＡＢの点間距離でこれを求めて「Ｍ」に記憶させる。辺長ＡＰと辺長ＢＰの値も余弦定理で使用するため，それぞれ「ｘ」と「ｙ」に記憶させておく。

③ＡとＢの点間距離を求め，Ｍに記憶させる
Abs(Ａ－Ｂ→Ｍ

④辺長ＡＰをｘに記憶させる
40→ｘ

⑤辺長ＢＰをｙに記憶させる
20→ｙ

メモリ名で余弦定理の図を書くと，以下のようになる。

アークコサインを使用し，上の式を解く。

⑥３辺の長さが既知の三角形の内角θを求めて，Ｃに記憶させる
Ｍ²＋ｘ²－ｙ²＝
Ans÷(2Ｍｘ＝
cos^-1(Ans→Ｃ

最後に，ＡからＢの方向角にθを加えて40ｍ移動した点を求めることで，Ｐ点の座標値を計算する。

①ＡからＢの方向角を求める
Arg(Ｂ－Ａ＝

②方向角と距離で座標を出す
Ａ＋40∠(Ans＋Ｃ＝

以上により，Ｐ点の座標値は，Ｘ座標24，Ｙ座標32と求められた。
よって，正解は「３」である。

問３＜基準点成果情報＞

基準点成果情報に関する正誤問題である。

１　〇
４級基準点280821から280820までの方向角が20°10′12.2″であり，280822までの方向角が217°23′42.5″であるため，２点の夾角は，217°23′42.5″－20°10′12.2″＝197°13′30.3″となる。

２　〇
４級基準点280821の経度は座標原点よりも小さいため，西に位置することが分かる。さらに，縮尺係数が0.999901で1.0000未満なので，東西方向に座標原点から90km未満に位置していることが分かる。

３　×
真北方向角が0°2′45.2″であるため，方位角（「真北」方向から時計回りに測定した側線への角）は，方向角－真北方向角で求めることができる。よって，20°10′12.2″－0°2′45.2″＝20°7′27.0″が方位角となる。

４　〇
標高にジオイド高を加えると楕円体高になるため，60.300＋36.616＝96.916ｍが楕円体高となる。

５　〇
基準点成果情報にある距離は，球面距離である。球面距離に縮尺係数をかけることで平面距離を計算することができるため，49.957×0.999901＝49.952…が平面距離となる。

よって，正解は「３」である。

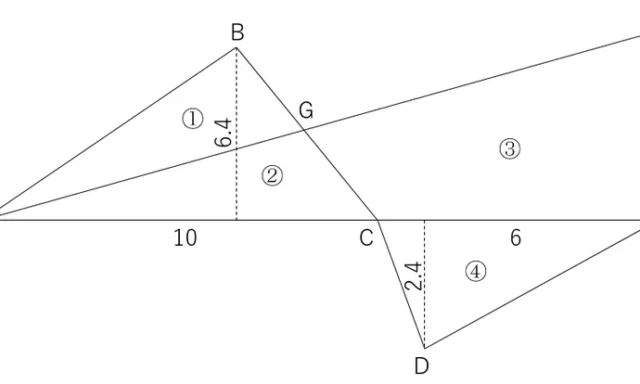
問４＜面積分割＞

三角形ABCのうち，三角形ABDの面積が108.10㎡になるＤ点の位置を求める。
三角形ABCの面積は，以下のようになる。

①Ａ点をＡに記憶させる
335.51＋287.44ｉ→Ａ

②Ｂ点をＢに記憶させる
332.9＋299.95ｉ→Ｂ

③Ｃ点をＣに記憶させる
315.15＋282.2ｉ→Ｃ

②三角形ABCを求積する
Conjg(Ａ)Ｂ＋Conjg(Ｂ)Ｃ＋Conjg(Ｃ)Ａ＝
Ans÷2＝
ImP(Ans＝

以上により，三角形ABCの面積が134.19㎡と求められた。
次に，ＣＢ間の距離を1としたときの，ＤＢ間の内分割合を求める。

①ＣＢ間の距離を1としたときの，ＤＢ間の内分割合を求め，Ｍに記憶させる
108.1÷134.19→Ｍ

①ＢからＣの距離を求める
Abs(Ｃ－Ｂ＝

②ＢからＤの距離を求め，Ｍに記憶させる
Ans×Ｍ→Ｍ

③ＢからＣの方向角を求める
Arg(Ｃ－Ｂ＝

④Ｄ点の座標値を求める
Ｂ＋Ｍ∠Ans=

以上によりＰ点の座標値は，Ｘ座標318.601…Ｙ座標285.651…と求められた。
よって，正解は「４」である。

問５＜交点計算＞

まずは，Ａ，Ｂ，Ｃ点をそれぞれメモリ「Ａ」，「Ｂ」，「Ｃ」に記憶させる。

①Ａ点をＡに記憶させる
100＋100ｉ→Ａ

②Ｂ点をＢに記憶させる
94.97＋97.5ｉ→Ｂ

③Ｃ点をＣに記憶させる
96＋103.18ｉ→Ｃ

交点Ｐは，Ｂ点からＣ点の方向にＢ点から出した直線と，Ｂ点からＣ点の方向に90°加えた方向にＡ点から出した直線の交点となる。交点計算をする場合は，下のようなメモを書く。

ＢからＣの方向角を「ｘ」に，ｘに90°加えたＡからの方向角を「ｙ」に記憶させる。

①ＢからＣの方向角を求め，ｘに記憶させる
Arg(Ｃ－Ｂ→ｘ

②Ａからの方向角を求め，ｙに記憶させる
Ans＋90→ｙ

③方向角ｘを加工して，ｘに記憶させなおす
tan(ｘ)＋ｉ→ｘ

④方向角ｙを加工して，ｙに記憶させなおす
tan(ｙ)＋ｉ→ｙ

⑤交点ＣのＸ座標を求めて，Ｄに記憶させる
Ｂｘ－Ａｙ＝
Ans÷(ｘ－ｙ＝
ReP(Ans→Ｄ

実部を抽出し，「Ｄ」に記憶させた。この値が交点ＰのＸ座標となる。

⑥交点ＰのＹ座標を求めて，Ｄに記憶させる
Ans－Ｂ＝
Ans×ｘ＝
ReP(Ans)ｉ＋Ｄ→Ｄ

以上によりＰ点の座標値は，Ｘ座標95.569…Ｙ座標100.803…と求められた。
最後に，Ａ点からＰ点の距離を求める。

①Ａ点からＰ点の距離を求める
Abs(Ｄ－Ａ＝

以上によりＡ点からＰ点の距離は，4.503…と求められた。
よって，正解は「２」である。

▲まとめ に戻る！▲