問11　小問１＜座標計算＞

まずは，Ｅ点とT1をそれぞれメモリ「Ｅ」，「ｘ」に記憶させる。

①Ｅ点をＥに記憶させる
29.57＋38.02ｉ→Ｅ

②T1をｘに記憶させる
24.99＋42.6ｉ→ｘ

次に，T1からＥ点の方向角から，T1からT2の方向角を引き，水平角を求める。
なお，T1からT2の方向角は問題文から196°である。

①T1からＥの方向角を求める
Arg(Ｅ－ｘ＝

②T1からＡ点の方向角から，T1からT2の方向角を引き，水平角を求める
Ans－(196＝
Ans＋360＝

以上により，T2を後視としたT1からＥ点までの水平角は119°と求められた。
最後に，T1からＥ点までの距離を求める。

①T1からＥ点までの距離を求める
Abs(Ｅ－ｘ＝

以上により，T1からＥ点までの距離は6.477…ｍと求められた。
よって，正解は，水平角が「119度」，四捨五入した距離が「6.48ｍ」である。

問11　小問２＜逆計算＞

距離ＢＤとＣＤを用いた逆計算により∠CBDを求めることになる。

まずは，Ｂ点とＣ点をそれぞれメモリ「Ｂ」と「Ｃ」に記憶させる。

①Ｂ点をＢに記憶させる
20.95＋10.44ｉ→Ｂ

②Ｃ点をＣに記憶させる
27.95＋10.44ｉ→Ｃ　

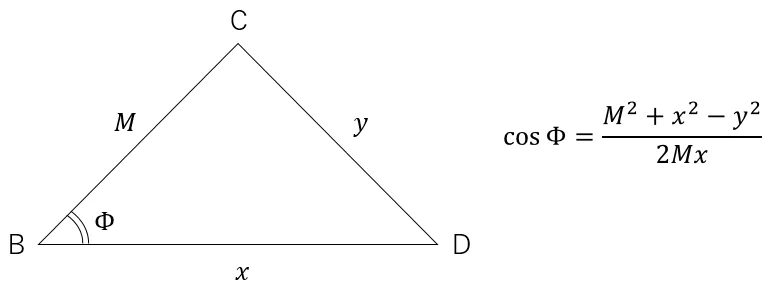
Ｂ点，Ｃ点及びＤ点をつなぐ三角形と見た場合，辺長ＢＤと辺長ＣＤは問題文の通りであるが，辺長ＢＣが不明なため，ＢＣの点間距離でこれを求めて「Ｍ」に記憶させる。辺長ＢＤと辺長ＣＤの値も余弦定理で使用するため，それぞれ「ｘ」と「ｙ」に記憶させておく。

③ＢとＣの点間距離を求め，Ｍに記憶させる
Abs(Ｂ－Ｃ→Ｍ

④辺長ＢＤをｘに記憶させる
15→ｘ

⑤辺長ＣＤをｙに記憶させる
13→ｙ

メモリ名で余弦定理の図を書くと，以下のようになる。

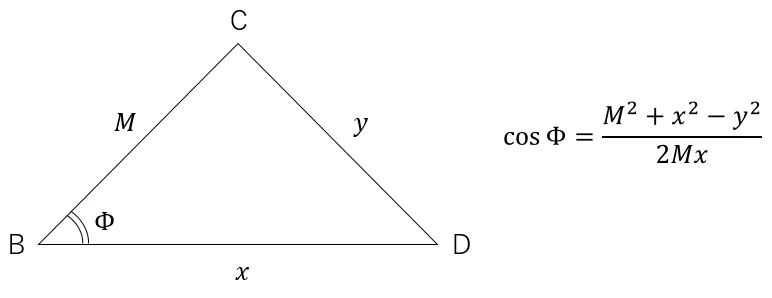
アークコサインを使用し，上の式を解く。

⑥３辺の長さが既知の三角形の内角θを求めて，Ｄに記憶させる
Ｍ²＋ｘ²－ｙ²＝
Ans÷(2Ｍｘ＝
cos^-1(Ans→Ｄ

以上により，∠CBDは60°と求められた。
よって，正解は「60度」である。

問11　小問３＜放射計算＞

ＢからＣの方向角に小問２で求めたθを加えて15ｍ移動した点を求めることで，Ｄ点の座標値を計算する。

①ＢからＣの方向角を求める
Arg(Ｃ－Ｂ＝

②方向角と距離で座標を出す
Ｂ＋15∠(Ans＋Ｄ＝

③Ｄ点の座標値を四捨五入し，Ｄに上書きする
38.45＋23.43ｉ→Ｄ

以上により，Ｄ点の座標値は，Ｘ座標38.45，Ｙ座標23.43と求められた。
よって，正解は，Ｘ座標「38.45」，Ｙ座標「23.43」である。

問11　小問４＜求積＞

土地を構成する座標値であるＡ，Ｆ，Ｇ，Ｈを，それぞれメモリ「Ａ」，「Ｆ」，「ｘ」，「ｙ」に記憶させる。

①Ａ点をＡに記憶させる
10.72＋12.19ｉ→Ａ

②Ｆ点をＦに記憶させる
20.57＋39.01ｉ→Ｆ

③Ｇ点をｘに記憶させる
15.4＋37.69ｉ→ｘ

④Ｈ点をｙに記憶させる
13＋24.94ｉ→ｙ

⑤求積をおこなう
Conjg(Ｂ)Ｆ＋Conjg(Ｆ)ｘ＋Conjg(ｘ)ｙ＋Conjg(ｙ)Ａ＋Conjg(Ａ)Ｂ＝
Ans÷2＝
ImP(Ans＝

以上により土地の面積は，209.39675と求められた。
よって，小数点以下第３位を切り捨て，正解は「209.39㎡」となる。

問11　小問５＜作図＞

（省略）
縮尺，方位，点名，辺長の記載をする他，当該地に接する道路についても作図することに注意する。

▲まとめ に戻る！▲