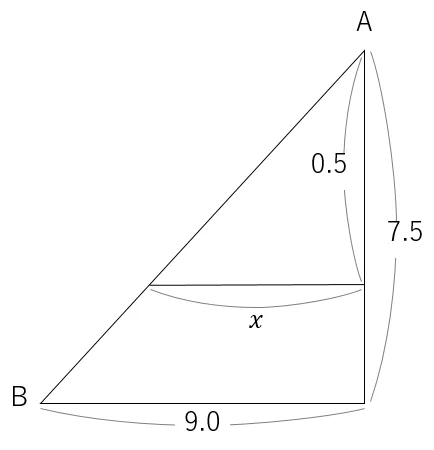
問６＜等高線の計算＞

比例による等高線の計算をする問題である。
問題文から，等高線は１ｍおきに表記されるとあるため，Ａ点からもっとも近い等高線は，66ｍとなる。

ＢからＡの高さは，66.5－59＝7.5ｍとなる。
等高線からＡの高さは，66.5－66＝0.5ｍとなる。

ＢからＡまでの距離は90ｍであるが，地形図の縮尺が1/1,000であるため，地図上の距離は，90.0ｍ÷1000＝0.090ｍ＝9.0cmとなる。

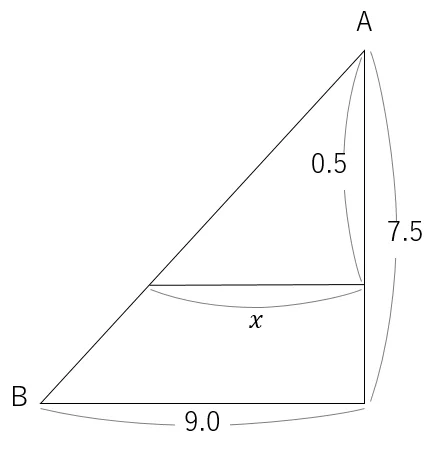
等高線からＡまでの地図上の距離をｘとおき，比例式にすると以下のとおりになる。

　7.5ｍ：9.0cm＝0.5ｍ：ｘcm

これを変形し，計算をしてｘを求める。

　ｘ＝9.0×0.5÷7.5
　　＝0.6cm

よって，正解は「２」である。

問７＜データの形式＞

データの形式に関する正誤問題である。

ア　×
ラスタデータは，一定の大きさの画素を並べたデータのため，拡大表示すると線の太さが太くなる。

イ　〇
ラスタデータとベクタデータは相互に変換することができる。ただし，変換すると画質や精度が落ちることがある。

ウ　×
道路中心線のベクタデータを用いれば，道路ネットワークを構築することによって，道路上の２点間の経路検索がおこなえる。よって，ラスタデータよりもベクタデータの方が適している。

エ　〇
ラスタデータとベクタデータは相互に変換することができ，GISでの重ね合わせをすることができる。

オ　〇
ベクタデータとは，図形を座標値と方向で表現するデータ形式である。点，面，線を表現することができる。

よって，誤っているものはア，ウであり，その組合せは「１」である。

問８＜機器の点検（三点法）＞

三点法による測定距離の補正を計算する問題である。

距離の補正値（器械定数と反射鏡定数の和）は，AC－（AB＋BC）で求まる。
なお，反射鏡定数は問題文から＋0.02である。

①器械定数と反射鏡定数の和を求める
1000.45－(650.25＋350.15＝

②器械定数を求める
Ans－.02

以上により，器械定数は＋0.03と求められた。
よって，正解は「３」である。

問９＜標高計算＞

水準測量の観測値から，閉合差を調整する問題である。
まずは，前の水準点の標高に高低差を加えていき，各水準点の観測標高を順次求める。

　BM1の観測標高＝72.52＋2.562＝75.082
　BM2の観測標高＝75.082＋－0.585＝74.497
　BM3の観測標高＝74.497＋5.226＝79.723
　Ｂの観測標高＝79.723＋－0.223＝79.500

以上により，Ｂの観測標高は79.500ｍと求められた。
実際の標高は問題から79.470ｍであるため，全体の補正量は，79.470－79.500＝－0.030ｍとなる。
これを，各水準点ごとに，累加距離÷路線距離で割り振る。路線距離は，0.8＋0.6＋0.9＋0.7＝3である。

　BM1の補正量＝－0.030×0.8÷3＝－0.008
　BM2の補正量＝－0.030×(0.8＋0.6)÷3＝－0.014
　BM3の補正量＝－0.030×(0.8＋0.6＋0.9)÷3＝－0.023
　Ｂの補正量＝全体の補正量＝－0.030

この補正量を観測標高に加えることで，標高の最確値を求めていく。

　BM1の標高＝75.082－0.008＝75.074
　BM2の標高＝74.497－0.014＝74.483
　BM3の標高＝79.723－0.023＝79.700
　Ｂの標高＝79.500－0.030＝79.470

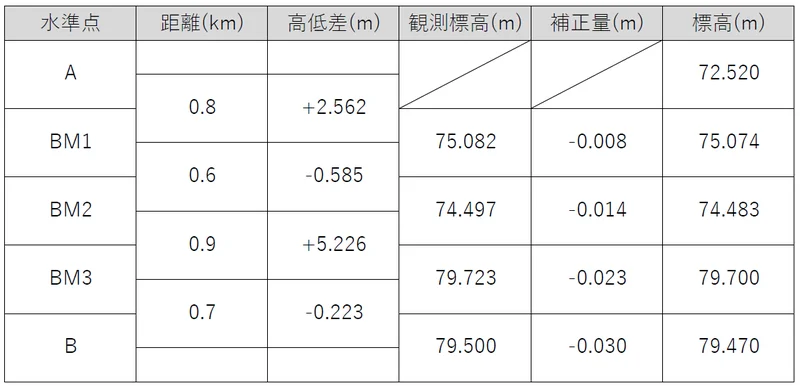
以上により，BM3の標高は79.700ｍと求められた。
よって，正解は「１」である。

問10＜座標計算＞

Ａ点の座標値を，Ｘ座標100，Ｙ座標100とし，Ａ点からＢ点の方向角を0°とすることで，座標計算によりＢ点とＣ点の座標値を求める。

①Ａ点をＡに記憶させる
100＋100ｉ→Ａ

②Ｂ点の座標値を求め，Ｂに記憶させる
Ａ＋22.749→Ｂ

③Ｃ点の座標値を求め，Ｃに記憶させる
Ａ＋24.12∠85→Ｃ

３点の座標値を使い，ＢＣ間の距離と三角形ＡＢＣの面積をそれぞれ求める。

①ＢからＣの距離を求める
Abs(Ｃ－Ｂ＝

②三角形ＡＢＣの面積を求める
Conjg(Ａ）Ｂ＋Conjg(Ｂ）Ｃ＋Conjg(Ｃ）Ａ＝
Ans÷2＝
ImP(Ans)＝

以上により，ＢＣ間の距離は31.680…ｍ，三角形ＡＢＣの面積は273.308…㎡と求められた。
よって，正解は「３」である。


▲まとめ に戻る！▲