問１＜閉合差＞

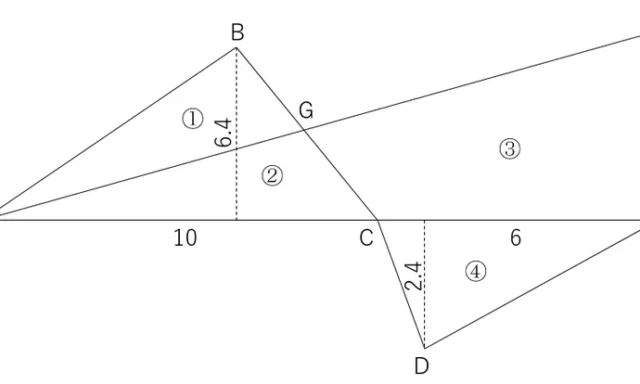
観測方向角の閉合差を計算する問題である。
まずは，それぞれの観測方向角を順次計算していき，Ａ点からＢ点の観測方向角を求める。

①Ｂ点からＣ点の観測方向角を求める
52＋257°40°35°－180＝

②Ｃ点からＤ点の観測方向角を求める
Ans＋253°20°45°－180＝

③Ｄ点からＥ点の観測方向角を求める
Ans＋262°25°10°－180＝

④Ｅ点からＡ点の観測方向角を求める
Ans＋240°13°5°－180＝

⑤Ａ点からＢ点の観測方向角を求める
Ans＋246°20°50°－720＝

次に，閉合差を求める。閉合差は，観測方向角から方向角を引くことで求められる。

Ans－52＝

以上により，Ａ点からＢ点の観測方向角の閉合差は0°0′25″と求められた。
よって，正解は「４」である。

問２＜間接水準測量＞

間接水準測量によって新点の標高を計算する問題である。
αAとαBの２つの鉛直角が観測されているため，既知点と新点で同時に観測を行う同時観測による間接水準測量である。
同時観測による間接水準測量の場合は両差の影響を相殺することができるため，２つの観測結果を平均すればよい。

同時観測による間接水準測量では，以下の式で新点Ｂの標高（HB）を求めることができる。

　HB＝HA＋iA=fA－（sin((－αA＋αB)÷2)×1250)－iB=fB

代入すると，以下のようになる。

　HB＝525＋1.32－(sin((15°0°15°＋14°59°45°)÷2)×1250)－1.24

以上により，新点Ｂの標高（HB）は201.556…と求められた。
よって，正解は「４」である。

問３＜座標変換＞

Ａ点とＢ点をA’点とB’点に移動・回転・伸縮した場合のＣ点の座標値を求める。
まずは，Ａ，Ｂ，Ｃ点及びA’点とB’点を，それぞれ「Ａ」，「Ｂ」，「Ｃ」，「Ｄ」，「Ｅ」に記憶させる。

①Ａ点をＡに記憶させる
200＋200ｉ→Ａ

②Ｂ点をＢに記憶させる
245＋245ｉ→Ｂ

③Ｃ点をＣに記憶させる
259.79＋225.38ｉ→Ｃ

④A’点をＤに記憶させる
－30－30ｉ→Ｄ

⑤B’点をＥに記憶させる
－30＋33.64ｉ→Ｅ

ＡＢの方向角・距離と，A’B’の方向角・距離を比較し，移動だけでなく，回転や伸縮があるかを調べる。

①ＡからＢの方向角を求める
Arg(Ｂ－Ａ＝

②A’からB’の方向角を求め，ＡからＢの方向角と比較し，差をｘに記憶させる
Arg(Ｅ－Ｄ)－Ans→ｘ

ここで求められたｘ（45°）が回転量となる。
次に，伸縮を調べる。

①ＡからＢの距離を求める
Abs(Ｂ－Ａ＝

②A’からB’の方向角を求め，ＡからＢの方向角と比較し，差をｙに記憶させる
Abs(Ｅ－Ｄ)÷Ans→ｙ

ここで求められたｙ（1.000006123）が伸縮量となる。
ただし，伸縮量は僅かであるため，伸縮はないものと考えてよい。

これらをもとに，座標変換後のＣ点の座標値を求める。
まずは，変換前のＡ点からＣ点までの方向角を計算する。

①ＡからＣの方向角を求める
Ang(Ｃ－Ａ＝

この水平角にｘを加えたものが，変換後のA’からC’の方向角となる。

②A’からC’の方向角を求め，ｘに記憶させる
Ans＋ｘ→ｘ

次に，変換前のＡ点からＣ点までの距離を計算する。

①ＡからＣの距離を求める
Abs(Ｃ－Ａ＝

この距離にｙをかけたものが，変換後のA’からC’の距離となる。

②A’からC’の距離を求め，ｙに記憶させる
Ans×ｙ→ｙ

最後に，変換後のA’からC’の方向角・距離で，C’の座標を求める

①C’の座標値を求める
Ｄ＋ｙ∠ｘ＝

以上により，C’点の座標値は，Ｘ座標－5.668…Ｙ座標30.224…と求められた。
よって，正解は「４」である。

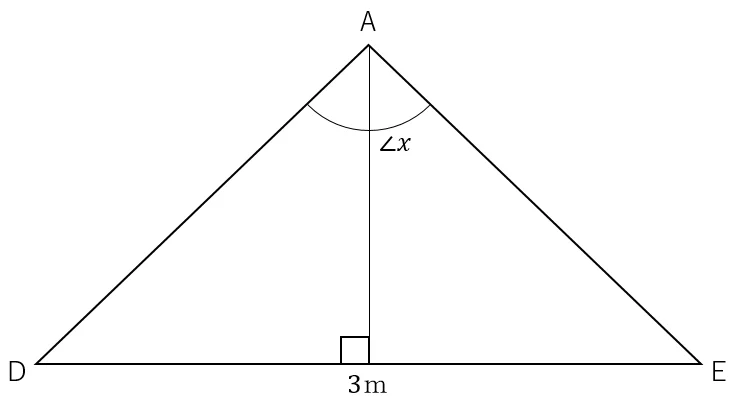
問４＜隅切り計算＞

Ａ，Ｂ，Ｃ点の座標値から∠BAEを求める。
まずは，Ａ，Ｂ，Ｃ点をそれぞれメモリ「Ａ」，「Ｂ」，「Ｃ」に記憶させる。

①Ａ点をＡに記憶させる
216.69＋209.11ｉ→Ａ

②Ｂ点をＢに記憶させる
205.2＋203ｉ→Ｂ

③Ｃ点をＣに記憶させる
214.63＋220.79ｉ→Ｃ

次に，Ａ点からＢ点の方向角から，Ａ点からＣ点の方向角を引き，∠BAEを求める。

④ＡからＢの方向角を求める
Arg(Ｂ－Ａ＝

⑤∠BAEを求め，ｘに記憶させる
Ans－Arg(Ｃ－Ａ＝
Ans＋360→ｘ

求めるべきＡＤの距離は，ＤＥの距離（3ｍ）の半分をsin(ｘ/2)で割ったものとなる。

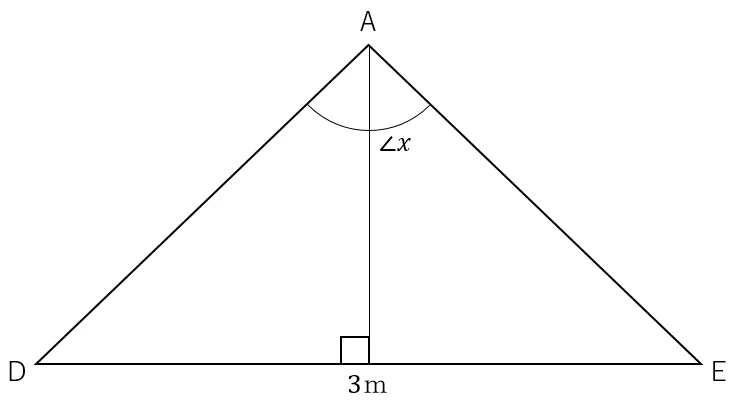
①ＡＤの距離を求める
sin(ｘ÷2＝
3÷2÷Ans＝

以上により，ＡＤの距離は，1.854…と求められた。
よって，正解は「４」である。

問５＜内分点＞

まずは，Ｃ点の座標値を求める。

①Ａ点をＡに記憶させる
312.51＋102.15ｉ→Ａ

②Ｂ点をＢに記憶させる
303.23＋122.46ｉ→Ｂ

③ＡからＢの方向角を求める
Arg(Ｂ－Ａ＝

④Ｃ点の座標値を求め，Ｃに記憶させる
Ｂ＋2∠Ans→Ｃ

以上により，Ｃ点の座標値が求まったため，Ａ点とＣ点を1：2に内分するＰ点の座標値を求める。

⑤Ｐ点の座標値を求める
Ｃ－Ａ＝
Ans÷３＋Ａ＝

以上により，Ｐ点の座標値は，Ｘ座標309.139…Ｙ座標109.526…と求められた。
よって，正解は「３」である。

▲まとめ に戻る！▲