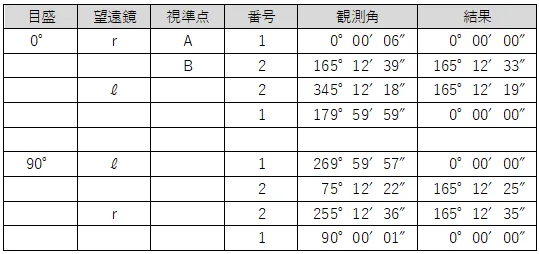
問６＜方向角計算（水平角の補正）＞

観測値から方向角を計算し，閉合差を配分して調整する。

Ａ点からP1，P1からP2，P2からＢ点，Ｂ点からＤ点と，順次方向角を求めていく。
なお，P1からP2の方向角は最後に調整するため，ｘに記憶させておく。

①Ａ点からP1の方向角を求める
345°57°50°＋152°15°14°＝
Ans－360＝

②P1からP2の方向角を求めてｘに記憶させる
Ans＋95°23°42°＝
Ans－180→ｘ

③P2からＢ点の方向角を求める
Ans＋179°52°30°＝
Ans－180＝

④Ｂ点からＤ点の方向角を求める
Ans＋160°35°34°＝
Ans－180＝

以上により求まった観測値と，実際の34°04′58″との差が誤差となる。
この誤差を観測点数（4）で割り，調整量を求める。

①調整量を求める
34°4°58°－Ans＝
Ans÷4＝

求めるべきP1からP2の方向角の観測は観測点数2なので，調整量に2をかけ，ｘに加えることで調整後の方向角を計算する。
Ans×2＋ｘ＝

以上により，調整後のP1からP2の方向角は53°36′50″と求められた。
よって，正解は「２」である。

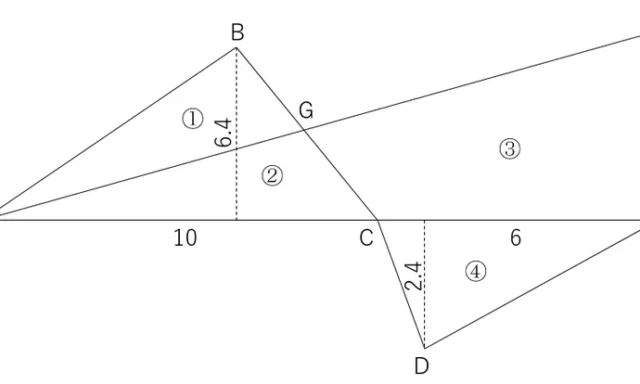
問７＜求積＞

観測値から，座標法により求積する問題である。

まずは，既知点をＸ座標100，Ｙ座標100とし，メモリ「Ｍ」に記憶させる。

①既知点をＭに記憶させる
100＋100ｉ→Ｍ

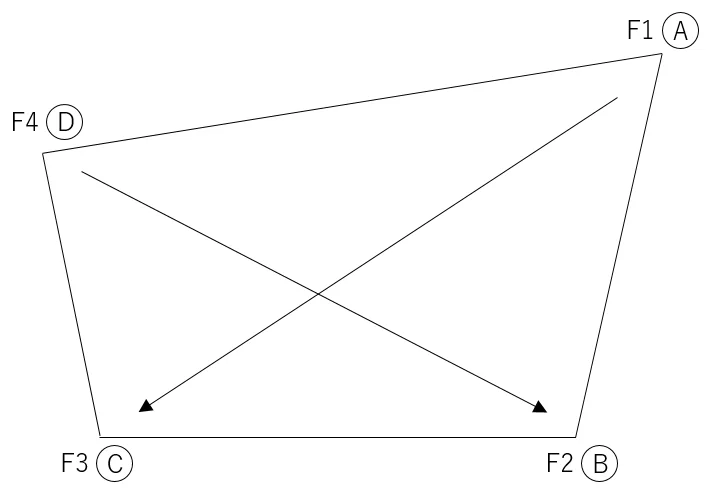
既知点から順次，放射によりF1からF4の座標値を求めていく。求めたF1からF4は，それぞれメモリ「Ａ」から「Ｄ」に記憶させる。なお，問題文に指定のある通り，求積前に小数点以下第３位を四捨五入する。

①F1の座標値を求めてＡに記憶させる
Ｍ＋36∠60＝
118＋131.18ｉ→Ａ

②F2の座標値を求めてＢに記憶させる
Ｍ＋22∠135＝
84.44＋115.56ｉ→Ｂ

③F3の座標値を求めてＣに記憶させる
Ｍ＋22∠225＝
84.44＋84.44ｉ→Ｃ

④F4の座標値を求めてＤに記憶させる
Ｍ＋22∠225＝
112.5＋78.35ｉ→Ｄ

四角形の土地であるため，簡易な方法で求積をおこなうことができる。
 

計算後の虚数部が土地の面積となる。

①求積をおこなう
Conjg(D－B)(A－C＝
Ans÷2＝
ImP(Ans＝

以上により土地の面積は，1280.146と求められた。
よって，正解は「１」である。

問８＜閉合比＞

閉合多角方式の閉合比を計算する問題である。

閉合比とは，閉合差と路線長の比であり，閉合差を路線長で割ることにより求める。
まずは，閉合差を計算する。
閉合差は，以下の式で求められる。

　閉合差＝√(合緯距－既知点のＸ座標)²＋（合経距－既知点のＹ座標）²

代入すると，以下のようになる。

　閉合差＝√(－425.23－－425.25)²＋(26.84－26.88)²

計算すると，閉合差は0.447…となる。
次に，閉合差を路線長で割ることで，閉合比を求める。分数の形式にすると，1/7050…と求められた。
よって，正解は「３」である。

問９＜GNSS測量における注意点＞

ア　×
スタティック法（短縮スタティック法）において基線の両端点で同じ機種のアンテナを使う場合は問題ないが，異なる機種のアンテナや電子基準点を用いる場合，アンテナの位相特性を補正するため，PCV補正（機種ごとに異なる電波の入射角によるアンテナの受信高の誤差を補正）をおこなう。

イ　〇
基線解析では，基線解析ソフトウェアで採用している標準値を用いて近似的に補正をおこなう。標準値を用いるため，観測点において測定した気温及び気圧の値を用いた気象補正は不要となる。なお，ネットワーク型RTK法では，基準局の観測データから作られる補正量などを取得し解析処理を行うことで軽減ができる。

ウ　×
衛星からの電波を受信するのはGNSS測量機のアンテナ部分であるため，アンテナから測点までの高さはミリメートル単位で計測しておく必要がある。高さは向きと異なり，各点で統一する必要はない。

エ　〇
電子基準点もGNSS測量機のアンテナと同様，衛星からの電波を受信していないと，正確な位置を示すことができない。そのため，電子基準点を既知点として使用する場合は，事前に電子基準点の稼動情況を確認しておく必要がある。

オ　×
多角測量では基準点の座標がなければ新点の座標が求まらないように，GNSS測量では，衛星の軌道情報は観測方法にかかわらず解析作業には不可欠となる。

よって，正しいものはイ，エであり，その組合せは「３」である。

問10＜重量平均による最確値＞

観測値から，重量平均による最確値を計算する問題である。

各路線におけるＥの標高を求めて，メモリ「Ａ」から「Ｄ」に記憶させる。

①Ｅ→Ａの標高を求めてＡに記憶させる
47.234－3.86→Ａ

②Ｅ→Ｂの標高を求めてＢに記憶させる
45.255－1.877→Ｂ

③Ｃ→Ｅの標高を求めてＣに記憶させる
41.452＋1.917→Ｃ

④Ｄ→Ｅの標高を求めてＤに記憶させる
38.744＋4.62→Ｄ

重量は路線長に反比例することから，各路線の観測距離から重量を求める。
　Ｅ→Ａの重量：Ｅ→Ｂの重量：Ｃ→Ｅの重量：Ｄ→Ｅの重量
　　＝1/2：1/4：1/1：1/2＝2/4：1/4：4/4：2/4
　　＝2：1：4：2

最後に，重量平均による最確値を求める。

①重量平均による最確値を求める
Ａ×2＋Ｂ×1＋Ｃ×4＋Ｄ×2＝
Ans÷(2＋1＋4＋2)＝

以上により最確値は，43.37ｍと求められた。
よって，正解は「３」である。


▲まとめ に戻る！▲