問１＜標準偏差＞

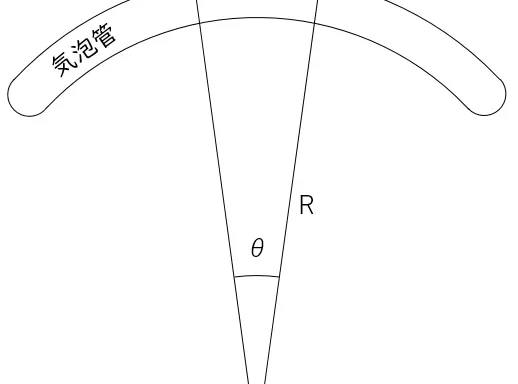
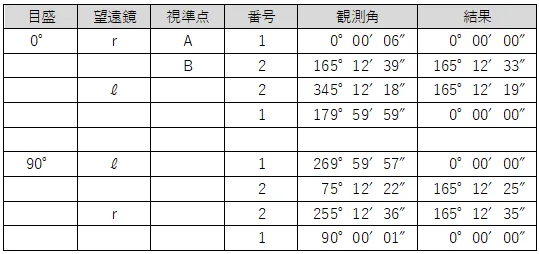
観測値から，標準偏差を計算する問題である。
標準偏差（M）は以下の式で求められる。n＝観測回数，v＝残差とする。残差とは，平均値と各観測値の差をいう。

また，最確値の標準偏差（M）は以下の式で求められる。

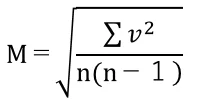
まずは，それぞれの観測値をメモリ「Ａ」から「Ｅ」までに記憶させる。
計算を簡略化するため，130°を基準とした。

①観測値１から５をＡからＥに記憶させる
－4→Ａ
5→Ｂ
－2→Ｃ
7→Ｄ
4→Ｅ

観測値の平均値を求める。

①観測値の平均値を求めてｘに記憶させる
Ａ＋Ｂ＋Ｃ＋Ｄ＋Ｅ＝
Ans÷5→ｘ

次に，各観測値の残差（v）を平均値から差し引くことで求める。
それぞれメモリ「Ａ」から「Ｅ」までに上書きする。

②観測値の残差を求める
Ａ－ｘ→Ａ
Ｂ－ｘ→Ｂ
Ｃ－ｘ→Ｃ
Ｄ－ｘ→Ｄ
Ｅ－ｘ→Ｅ

各観測値の残差を二乗して合計する。

③の残差を二乗して合計してｘに記憶させる
Ａ²＋Ｂ²＋Ｃ²＋Ｄ²＋Ｅ²→ｘ

はじめに，標準偏差を求める。

①標準偏差を求める
√(ｘ÷(5－1＝

以上により，標準偏差は4.743…と求められた。
次に，最確値の標準偏差を求める。

①最確値の標準偏差を求める
√(ｘ÷(5×(5－1＝

以上により，最確値の標準偏差は2.121…と求められた。
よって，正解は「２」である。

問２＜角度の偏心補正計算＞

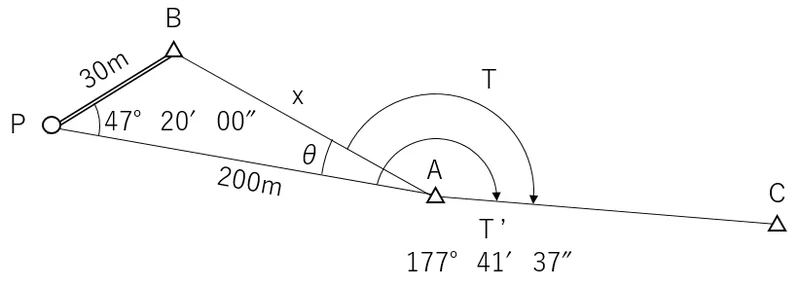
観測値から，角度の偏心補正計算をする問題である。
正弦定理を使用してθを求めるため，まずはＡＢ間の距離（ｘ）を求める。

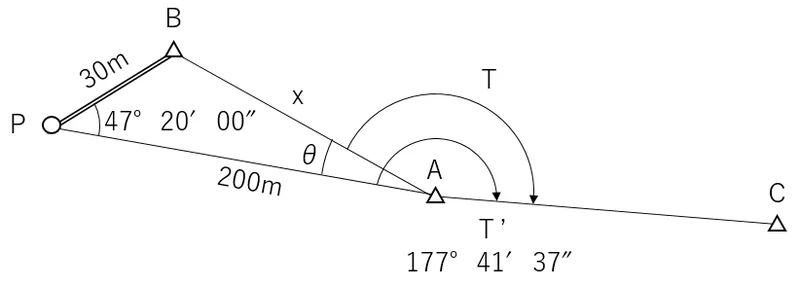
２辺の辺長と内角の１つが判明していため，第二余弦定理を使用する。

①ＡＢ間の距離（ｘ）を求めてｘに記憶させる
cos47°20°＝
Ans×2×200×30＝
Ans－(200²＋30²＝
√(Ans→ｘ
ｘ÷ｉ→ｘ

以上により，ｘの長さは181.017…となった。
次に，正弦定理によりθを求める。

正弦定理から，

　sinθ/e＝sinφ/ｘ となる。

代入すると，以下のようになる。

　sinθ/30＝sin47°20′/ｘ

①θの角度を求める
sin(47°20°)×30÷ｘ＝
sin^-1(Ans＝

②∠Ｔを求める
177°41°37°－Ans＝

問題文から，点Ａにおける点Ｂの方向角は324°36′23″であるため，これにＴ’を加えることで，点Ｃの方向角を求める。

①点Ｃの方向角を求める
324°36°23°＋Ans＝
Ans－360＝

以上により，点Ａにおける点Ｃの方向角は135°18′1.35″と求められた。
よって，正解は「１」である。

問３＜角度＞

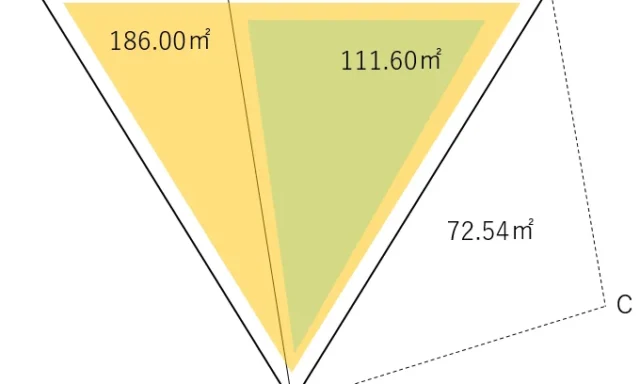
五角形ＡＢＣＤＥの面積と四角形Ａ’ＣＤＥの面積が等しいということは，三角形ＡＢＣと三角形Ａ’ＣＡの面積が等しいということになる。

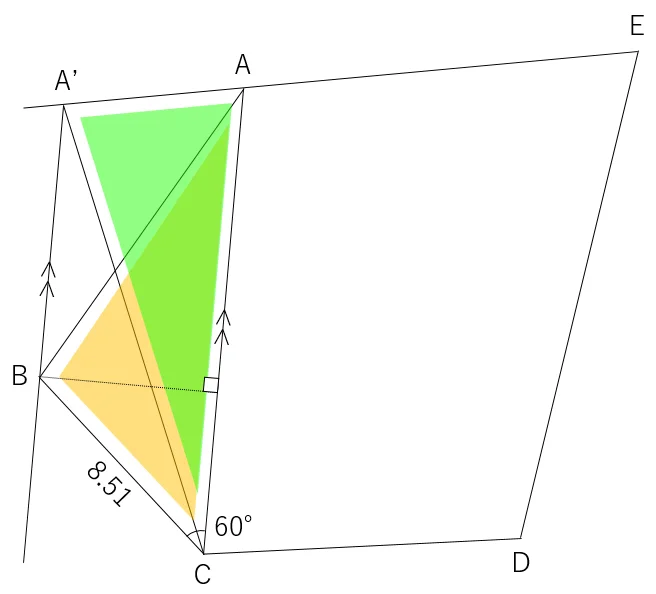
この２つの三角形は底辺をＡＣで共通とするため，面積を等しくするためには，高さが等しくなければならない。つまり，ＡＣとＢＡ’は平行ということになる。
また，この高さは，8.51×sin(60)＝7.369…ｍとなる。

次に，角度に着目する。
三角形の内角の和は180°であるため，∠BACは180－(100＋60)＝20°となる。
また，∠BAEが130°であるため，∠CAEは130－20＝110°となる。

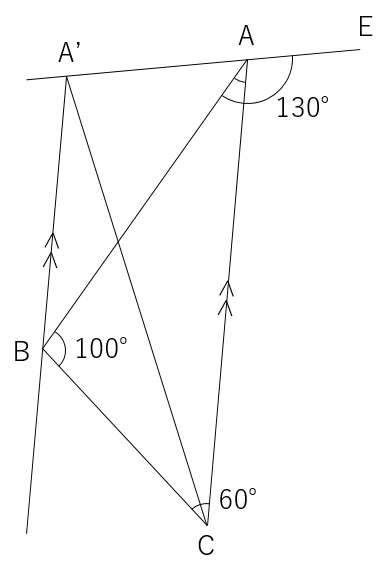
ＡＣとＢＡ’は平行であるため，∠CAEと∠BA’Aは等しく，110°となる。

Ａ’からＡＤに向けた垂線の交点をＦとすると，∠BA’Fが直角になるため，∠FA’Aは110－90＝20°となる。

​​​​​​​

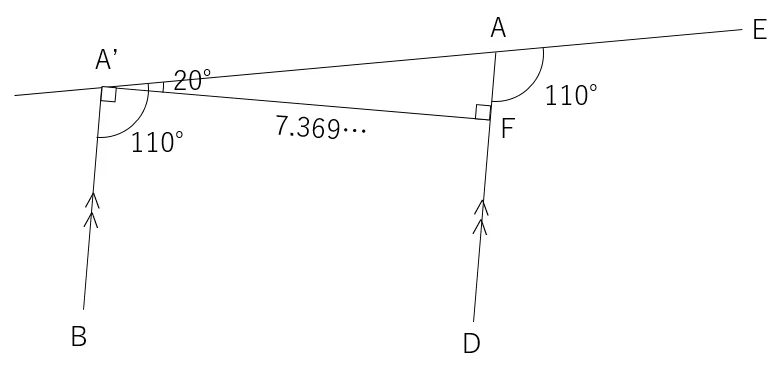
よって，三角形A’FAにおける三角関数を使い，Ａ’Ａの距離は，7.369…÷cos(20)＝7.842…と求められた。
よって，正解は「３」である。

問４＜距離の観測誤差＞

距離の観測誤差の正誤問題である。

１　〇
位相測定誤差は光波の周波数に誤差が比例するもので，測定距離には比例しない。

２　〇
変調周波数の誤差では，基準となる光の波長の長さを変えてしまうことから，変調周波数誤差は測定距離に比例する。

３　×
気温と気圧の変化が観測距離に与える影響では，気温の変化が与える影響の方が相対的に大きい。

４　〇
気温が高くなり分子密度が低くなるほど光の速度が早くなるため，実際の距離よりも観測距離は短くなる。

５　〇
気圧が高くなり分子密度が高くなるほど光の速度が遅くなるため，実際の距離よりも観測距離は長くなる。

よって，誤っているのは「３」である。

問５＜方向角計算＞

観測値から，方向角を計算する問題である。

まずは，T1，T2，T3の各点をそれぞれメモリ「Ａ」，「Ｂ」，「Ｃ」に記憶させる。

①T1をＡに記憶させる
148.23＋90.37ｉ→Ａ

②T2をＢに記憶させる
180.4＋102.72ｉ→Ｂ

③T3をＣに記憶させる
134.52＋60.97ｉ→Ｃ

T1からＰ点の方向角は，T1からT2の方向角から反時計回りに63°の角度となる。
よって，T1からT2の方向角を求めることで，Ｐ点の座標値を求めることができる。

①T1からT2の方向角を求めて，Ｄに記憶させる
Arg(Ｂ－Ａ＝
Ａ＋30.26∠(Ans－63→Ｄ

∠ＰT3T1をθとした場合，θは，T3からT1の方向角からT3からＰの方向角を引くことで求めることができる。

①T3からT1の方向角を求める
Arg(Ａ－Ｃ＝

②T3からT1の方向角からT3からＰの方向角を引く
Ans－Arg(Ｄ－Ｃ＝

βは360°からθを引いて求める。

①βを求める
360－Ans＝

以上により，βは309.190…°と求められた。
よって，正解は「２」である。


▲まとめ に戻る！▲