問６＜機器の点検（不等距離法）＞

不等距離法による標尺読定値の補正を計算する問題である。

位置Ｂのレベルによる標尺Ⅱの読定値と，位置Ａのレベルによる標尺Ⅰの読定値を＋にし，位置Ｂのレベルによる標尺Ⅰの読定値と，位置Ａのレベルによる標尺Ⅱの読定値を－にして足し合わせ，1.1をかけることで補正量を計算する。

①補正量を求める
1.222＋1.24－1.363－1.109＝
Ans×1.1＝

求めるべき位置Ｂのレベルによる標尺Ⅰの読定値に補正量を足し合わせることで，補正後の標尺読定値を計算する。

1.363＋Ans＝

以上により，補正後の位置Ｂのレベルによる標尺Ⅰの読定値は1.352と求められた。
よって，正解は「１」である。

問７＜観測手簿（水平角）＞

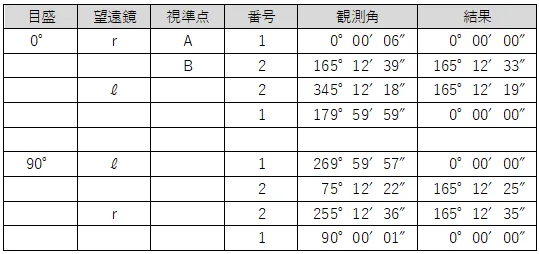
観測値から，水平角を計算する問題である。

まずは，「結果」を計算する。
結果は，新点（Ｂ）の観測角から基準となる点（Ａ）の観測角を引くことで計算する。

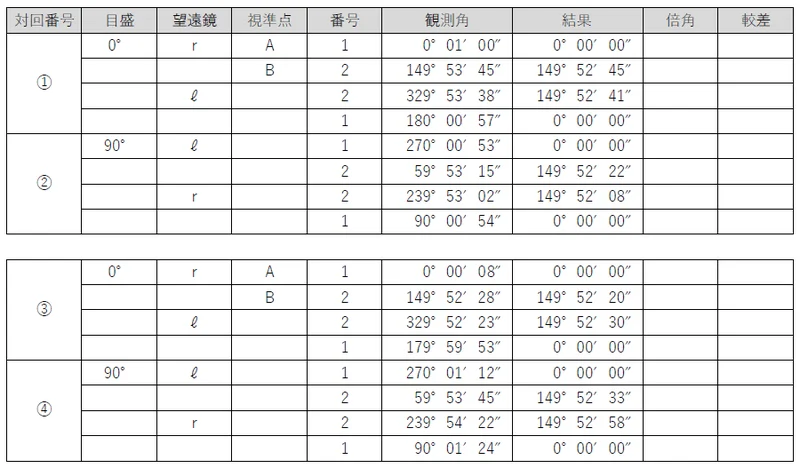
次に，対回ごとに，新点の結果について正反の合計を計算する。この値を「倍角」という。
通常は，秒の単位だけ合計すれば足りる。

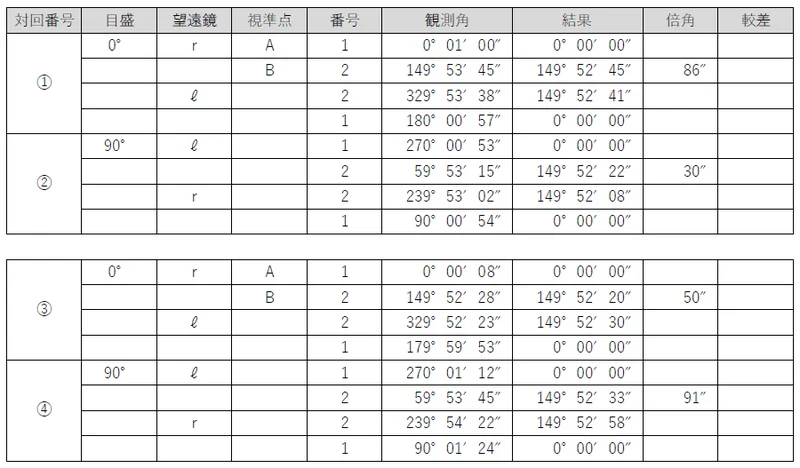
さらに，新点の結果について正（ｒ）の結果から反（ℓ）の結果を引く。この値を「較差」という。

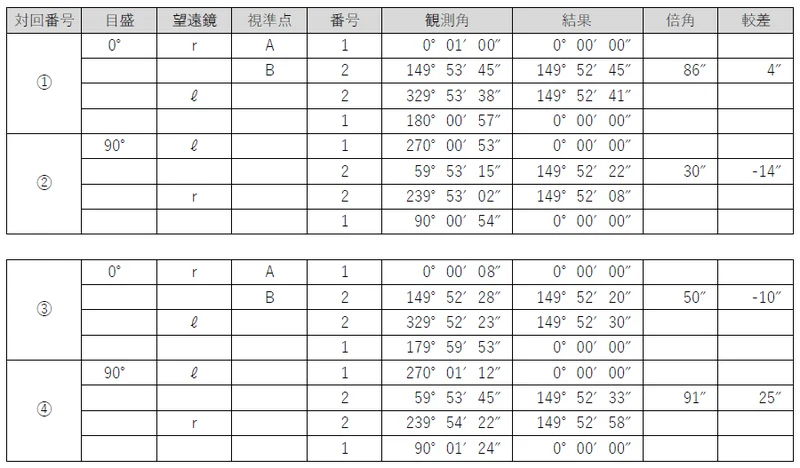
最後に，それぞれの対回の組合せごとの「倍角差」と「観測差」を計算する。
「倍角差」は，倍角の最大値から最小値を引くことで求められ，「観測差」は，較差の最大値から最小値を引くことで求められる。

許容値は，問題文から倍角差30″，観測差20″なので，これを満たす組合せは②③のみであるため，これを採用する。
対回番号②③のＢの結果は，149°52′22″，149°52′08″，149°52′20″，149°52′30″であるため，これを平均することで最確値を求める。
（ちなみに，「149°52′」までは４つの値で共通であるため，秒単位の計算で足りる。）

以上により，ＡからＢの水平角は，149°52′20″と求められた。
よって，正解は「４」である。

問８＜逆計算＞

逆計算により，座標値を求める問題である。
なお，∠Ｔが明らかなため，正弦定理を使用しても解ける。

まずは，Ａ点とＢ点をそれぞれメモリ「Ａ」と「Ｂ」に記憶させる。

①Ａ点をＡに記憶させる
200＋180ｉ→Ａ

②Ｂ点をＢに記憶させる
225.21＋225.48ｉ→Ｂ

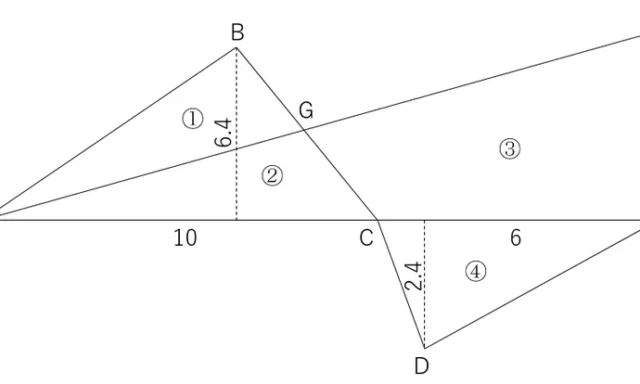
Ａ点，Ｂ点及びＣ点をつなぐ三角形と見た場合，辺長ＢＣと辺長ＡＣは問題文の通りであるが，辺長ＡＢが不明なため，ＡＢの点間距離でこれを求めて「ｘ」に記憶させる。辺長ＢＣと辺長ＡＣの値も余弦定理で使用するため，それぞれ「ｙ」と「Ｍ」に記憶させておく。

③ＡとＢの点間距離を求め，ｘに記憶させる
Abs(Ａ－Ｂ→ｘ

④辺長ＢＣをｙに記憶させる
44.1→ｙ

⑤辺長ＡＣをＭに記憶させる
41.24→Ｍ

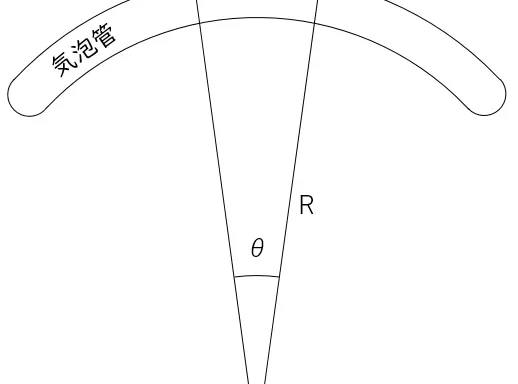
メモリ名で余弦定理の図を書くと，以下のようになる。

アークコサインを使用し，上の式を解く。

⑥３辺の長さが既知の三角形の内角θを求めて，Ｃに記憶させる
ｘ²＋Ｍ²－ｙ²＝
Ans÷(2ｘＭ＝
cos^-1(Ans→Ｃ

最後に，ＡからＢの方向角にθを加えて41.24ｍ移動した点を求めることで，Ｃの座標値を計算する。

①ＡからＢの方向角を求める
Arg(Ｂ－Ａ＝

②方向角と距離で座標を出す
Ａ＋41.24∠(Ans＋Ｃ＝

以上により，Ｃ点の座標値は，Ｘ座標181.920…Ｙ座標217.065…と求められた。
よって，正解は「１」である。

問９＜コンパス法によるトラバース調整＞

問題の図にあるＥ点からＡ点までの観測角と距離から，観測されたＡ点（ＡＤ）の座標値を求める。
まずは，Ｅ点とＤ点を，それぞれメモリ「Ｅ］と「Ｄ」に記憶させる

①Ｅ点をＥに記憶させる
－6.03＋5.92ｉ→Ｅ

①Ｄ点をＤに記憶させる
.18＋16.7→Ｄ

③Ｅから方向角と距離でＡＤの座標を出し，Ａに記憶させる
Ｅ＋8.52∠315°31°23°→Ａ

Ａ点の座標値からＡＤの座標値を引くことで，補正量を求める。

④補正量を求める
0－Ａ＝

コンパス法では各辺長で調整することとなるため。補正量を観測辺長の合計で割り，それに求める観測点（Ｄ）までの辺長の合計をかけて調整誤差を計算する。その調整誤差を観測結果に足すことで，最確値を求めることができる。

⑤コンパス法による閉合調整をする
Ans÷(8.2＋8.09＋9.77＋12.44＋8.52)×(8.2＋8.09＋9.77)＝

⑥Ｄを調整する
Ans＋Ｄ＝

以上により，調整後のＤ点の座標値は，Ｘ座標0.152…Ｙ座標16.727…と求められた。
よって，正解は「２」である。

問10＜座標計算＞

問題文に「取付観測をすることなく」とあるため，方向角ＡＢを使った放射計算をすることができない。
そのため，距離ＡT1とT1Ｃを用いた逆計算により座標値を求めることになる。

まずは，Ａ点とＣ点をそれぞれメモリ「Ａ」と「Ｃ」に記憶させる。

①Ａ点をＡに記憶させる
500＋500ｉ→Ａ

②Ｃ点をＣに記憶させる
506＋585ｉ→Ｃ

Ａ点，Ｃ点及びT1をつなぐ三角形と見た場合，辺長ＡT1と辺長T1Ｃは問題文の通りであるが，辺長ＡＣが不明なため，ＡＣの点間距離でこれを求めて「Ｍ」に記憶させる。辺長ＡT1と辺長T1Ｃの値も余弦定理で使用するため，それぞれ「ｘ」と「ｙ」に記憶させておく。

③ＡとＣの点間距離を求め，Ｍに記憶させる
Abs(Ａ－Ｃ→Ｍ

④辺長ＡT1をｘに記憶させる
50→ｘ

⑤辺長T1ＣをＭに記憶させる
51→ｙ

メモリ名で余弦定理の図を書くと，以下のようになる。

アークコサインを使用し，上の式を解く。

⑥３辺の長さが既知の三角形の内角θを求めて，Ｄに記憶させる
ｘ²＋Ｍ²－ｙ²＝
Ans÷(2ｘＭ＝
cos^-1(Ans→Ｄ

最後に，ＡからＣの方向角からθを引いて50ｍ移動した点を求めることで，T1の座標値を計算する。

①ＡからＣの方向角を求める
Arg(Ｃ－Ａ＝

②方向角と距離で座標を出す
Ａ＋50∠(Ans－Ｄ＝

以上により，T1点の座標値は，Ｘ座標530 Ｙ座標540と求められた。
よって，正解は「２」である。

▲まとめ に戻る！▲