問１＜交点計算＞

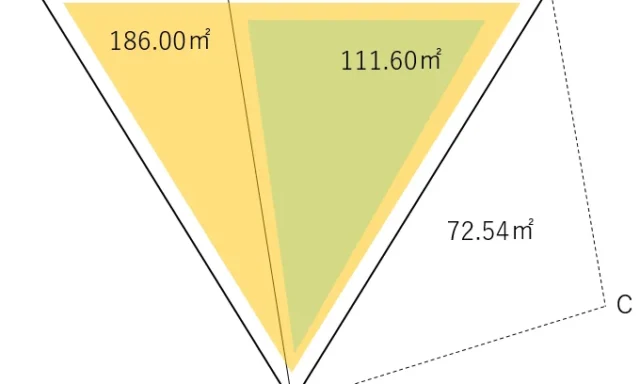
三角関数でも求めることができるが，ここでは複素数を使った交点計算で答えを求める。
方向角が90度の交点計算をするにあたり必要なのは，方向角90度以外の１点の座標値と，その点からの方向角である。

①Ｄ点をＤに記憶させる
94.33＋112.7ｉ→Ｄ

次に，Ｄ点からの方向角を計算し，メモリ「ｙ」に記憶させる

②ＤからＦの方向角を計算し，ｙに記憶させる
90＋225－360→ｙ

③方向角ｙを加工して，ｙに記憶させなおす
tan(ｙ)＋ｉ→ｙ

交点ＦのＸ座標は，点ＥのＸ座標と同一であるため，交点ＦのＸ座標は98であることが分かる。よって，通常の交点計算と同様に，このＸ座標を用いて交点ＦのＹ座標のみを計算すればよい。

④交点ＦのＹ座標を求める
98－Ｄ＝
Ans×ｙ＝

上段の実部の値（109.03）が，交点のＹ座標となる。
よって，正解は「３」である。

問２＜角＞

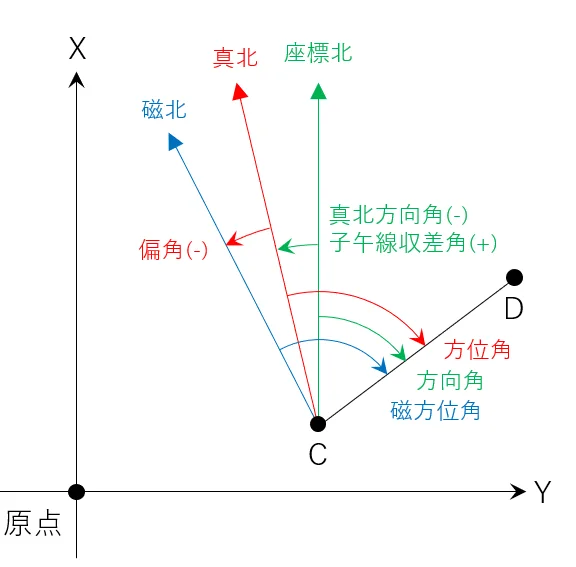
北を表す⽅向には，座標北，真北，磁北の３つがあり，以下のようになっている。

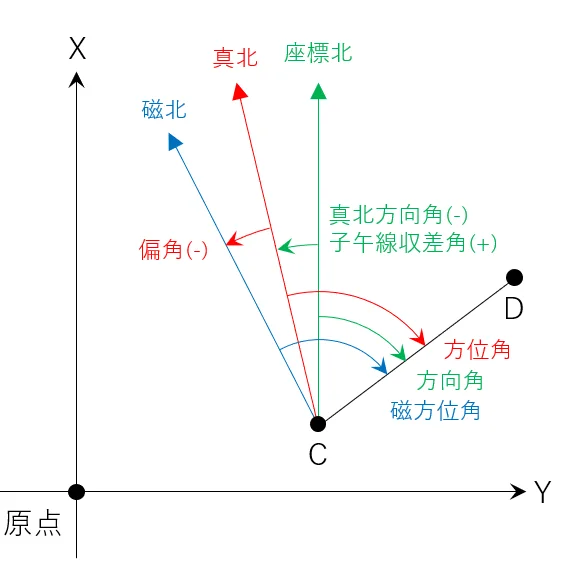
Ａ点を通る「磁北」方向から時計回りにＢ点を測定した側線への角を「磁方位角」という。
Ａ点を通る「真北」方向から時計回りにＢ点を測定した側線への角を「方位角」という。
Ａ点を通る「座標北」方向から時計回りにＢ点を測定した側線への角を「方向角」という。

Ａ点を通る「真北」方向から時計回りに「磁北」方向までの角度を「偏角」という。
Ａ点を通る「真北」方向から時計回りに「座標北」方向までの角度を「子午線収差」という。

よってアは「偏角」，イは「子午線収差」，ウは「方位角」，エは「方向角」となる。
よって，正解は「１」である。

問３＜機器の点検（三点法）＞

三点法による測定距離の補正を計算する問題である。

距離の補正値（器械定数と反射鏡定数の和）は，AC－（AB＋BC）で求まる。
なお，反射鏡定数は問題文から－0.025である。

①器械定数と反射鏡定数の和を求める
254.184－(131.667＋122.502＝

②器械定数を求める
Ans－－.025＝

以上により，器械定数は＋0.040と求められた。

次に，AC間の距離を補正する。①の計算は，↑キーを使って再計算すると良い。

①器械定数と反射鏡定数の和を求める
254.184－(131.667＋122.502＝

②AC間の補正後の距離を求める
254.184＋Ans＝

以上により，AC間の補正後の距離は254.199と求められた。
よって，正解は「５」である。

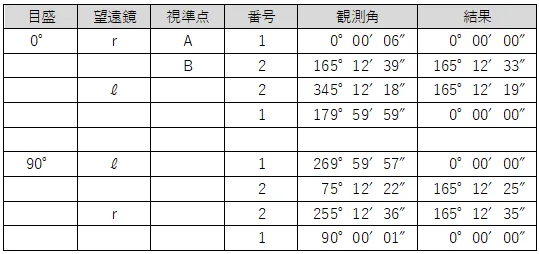
問４＜観測手簿（高低角）＞

観測値から，高低角を計算する問題である。

まずは，観測された鉛直角を平均し鉛直角の最確値を求める。
望遠鏡の反の観測値は360°から差し引くことに注意する。

①点Ｂの鉛直角の最確値を求める
89°15°35°＋(360－270°44°35°＝
Ans÷2＝
高低角は，90°から鉛直角の最確値を引いたものになる。

①点Ｂの高低角を求める
90-Ans＝

以上により，点Ｂの高低角は0°44′30″と求められた。
同様に，点Ｃについても計算する。

①点Ｃの鉛直角の最確値を求める
360－269°55°5°＋90°5°15°＝
Ans÷2＝

②点Ｃの高低角を求める
90-Ans＝

以上により，点Ｃの高低角は－0°5′5″と求められた。
よって，正解は「５」である。

問５＜平面距離＞

「平面距離」とは，平面直角座標系上の距離であり，「球面距離」（回転楕円体上の距離）に縮尺係数をかけることで求めることができる。
一方，「球面距離」は，観測された「水平距離」を投影補正することで求まる。

まずは，観測された「水平距離」を斜距離から求める。

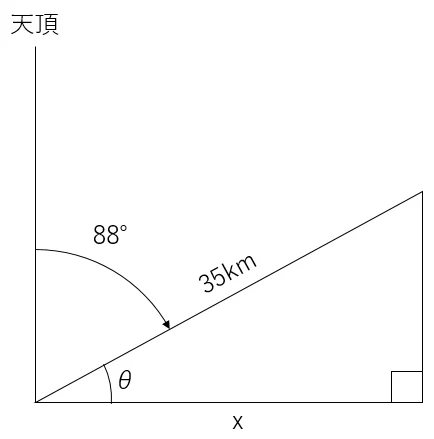
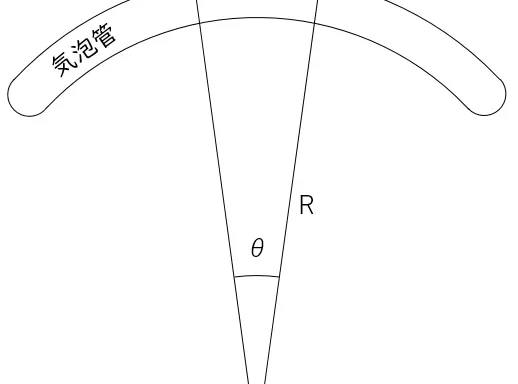
①角θを求める
90－88＝

②水平距離を計算し，ｘに記憶させる
cos(Ans)×35→ｘ

以上により，水平距離は34.97867895と求められた。
次に，投影補正をおこない，球面距離を求める。
投影補正のための補正量は，以下の式で求めることができる。

　投影補正量＝－(水平距離×平均標高÷地球半径)

①投影補正量を求める
ー(ｘ×1.6÷6370＝

補正量を水平距離に加えることで，投影後の球面距離を計算する。

②球面距離を計算する
ｘ＋Ans＝

最後に，球面距離に縮尺係数をかけ，平面距離を計算する。

Ans×.999925＝

以上により，平面距離は34.967…と求められた。
よって，正解は「３」である。

▲まとめ に戻る！▲