問11　小問１＜交点計算＞

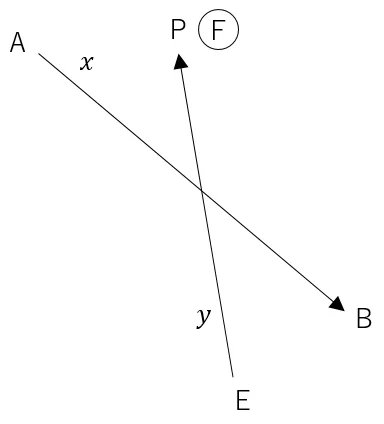
２直線の交点の座標を求める問題である。

Ｑ点は，ＡＢを結んだ直線と，ＥＰを結んだ直線の交点となる。交点計算をする場合は，下のようなメモを書く。

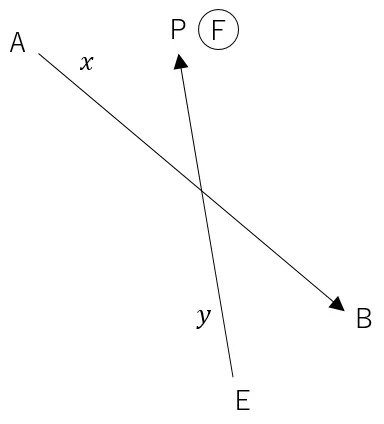
交点計算に必要なＡ，Ｂ，Ｅ及びＰ点を，それぞれメモリ「Ａ」，「Ｂ」，「Ｅ」，「Ｆ」に記憶させる。

①Ａ点をＡに記憶させる
113.5＋86.36ｉ→Ａ

②Ｂ点をＢに記憶させる
110.05＋100.16ｉ→Ｂ

③Ｅ点をＥに記憶させる
93.75＋101.1ｉ→Ｅ

④Ｐ点をＦに記憶させる
107.25＋98.94ｉ→Ｆ

ＡからＢの方向角を「ｘ」に，ＥからＦの方向角を「ｙ」に記憶させる。

①ＡからＢの方向角を求め，ｘに記憶させる
Arg(Ｂ－Ａ→ｘ

②ＥからＦの方向角を求め，ｙに記憶させる
Arg(Ｆ－Ｅ→ｙ

③方向角ｘを加工して，ｘに記憶させなおす
tan(ｘ)＋ｉ→ｘ

④方向角ｙを加工して，ｙに記憶させなおす
tan(ｙ)＋ｉ→ｙ

⑤交点ＱのＸ座標を求めて，Ｍに記憶させる
Ａｘ－Ｅｙ＝
Ans÷(ｘ－ｙ＝
ReP(Ans→Ｍ

実部を抽出し，「Ｍ」に記憶させた。この値が交点ＱのＸ座標となる。

⑥交点ＱのＹ座標を求めて，Ｍに記憶させる
Ans－Ａ＝
Ans×ｘ＝
ReP(Ans)ｉ＋Ｍ→Ｍ

以上によりＱ点の座標値は，Ｘ座標110.484…Ｙ座標98.422…と求められた。
よって，値を四捨五入し，正解はＸ座標「110.48」Ｙ座標「98.42」である。

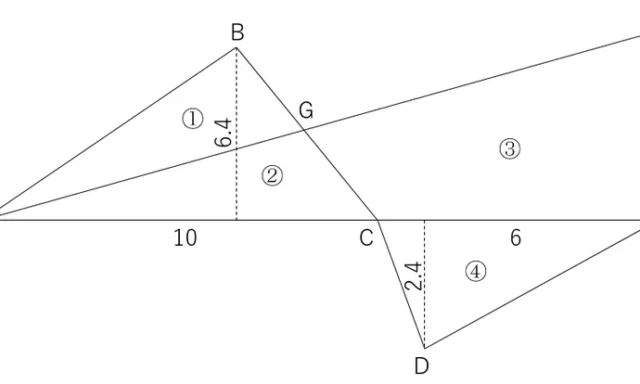
問11　小問２＜求積＞

まずは，土地を構成する座標値を順次メモリに入力する。すでにＢ点とＥ点については，それぞれ「Ｂ」と「Ｅ」に入力が済んでいる。

①Ｃ点をＣに記憶させる
111.6＋113.17ｉ→Ｃ

②Ｄ点をＤに記憶させる
95.12＋116.61ｉ→Ｄ

面積を求める土地は四角形の土地であるため，簡易な方法で求積をおこなうことができる。
計算後の虚数部が土地の面積となる。

①求積をおこなう
Conjg(Ｂ－Ｃ)(Ｄ－Ｅ＝
Ans÷2＝
ImP(Ans＝

以上により土地の面積は，236.9188と求められた。
よって，値を四捨五入し，正解は「236.92㎡」である。

問11　小問３＜方向角と距離＞

T1からＡ点までの方向角と距離を求める。
まずは，T1とＡ点の座標値をそれぞれメモリ「Ｍ」と「Ａ」に記憶させる。

①T1をＭに記憶させる
108.76＋90.78ｉ→Ｍ

②Ａ点をＡに記憶させる
113.5＋86.36ｉ→Ａ

T1からＡ点までの方向角を計算する。

①T1からＡ点までの方向角を求める

Arg(Ａ－Ｍ＝

これでT1からＡ点までの方向角が－42.999…と求められた。時計回りの方向角にするため，360を加え，正解は「317°」となる。
次に，距離を求める。

①T1からＡ点までの距離を求める

Abs(Ａ－Ｍ＝

これでT1からＡ点までの距離が6.481…と求められた。四捨五入をし，正解は「6.48ｍ」となる。

問11　小問４＜作図＞

（省略）
縮尺，方位，点名，辺長の記載をする他，当該地に接する道路についても作図することに注意する。


▲まとめ に戻る！▲